3

I'm trying to graph a series of planes as a solid object in Mathematica. I first tried to use the Plot3D options as well as the fill options to plot a $3D$ volume, but was unable to find a working result.

The graphics I'm trying to create will show the deviation between the $z$ axis and the radius from the origin of a $3D$ cuboid. The current equation I'm using is this:

Plot3D[Evaluate[{ Sqrt[(C[1])^2 + x^2 + y^2]} /. C[1] -> Range[6378100, 6379120]], 
         {x, -1000000, 1000000}, {y, -1000000, 1000000}, AxesLabel -> Automatic]

Where C1 was the original $z$-value at each plane and the result of this equation is $\; z+(r-z)\;$ for any point on the $(x,y)$-plane.

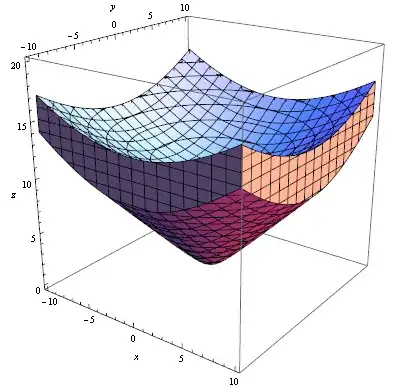
Output for more manageable range looks as follows

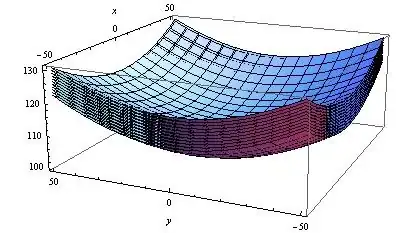
enter image description here

However this method is incredibly inefficient. Because this will be used to model large objects with an original $z$-values of $>6,000,000$ and heights above $1000$, Mathematica is unable to graph thousands of planes and represent them in a responsive method.

Additionally, because the Range of C1 only includes integer values, there is discontinuity between these planes.

Is there a way to rewrite this using different Mathematica functionality that will generate a $3D$-plot that is both a reasonable load on my system and is a smooth object?

2nd, What can I do to improve my perforamance? when computing the above input for $>30$min, Mathematica was only utilizing about $30$% CPU and $4$GB of ram with a light load on my graphics card as well. This is only about twice as much as Chrome is using right now on my system.

I attempted to enable CUDALink, but it wouldn't enable properly. Would this offer a performance boost for this type of processing?

For a reference, my system build is: $16$GB Ram Intel i7 4770K running at stock settings Nvidia GeForce 760GTX 256 Samsung SSD

I'm running Mathematica 9.

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
Everett Knag
  • 63
  • 3
  • CUDAlink doesn't let Mathematica magically run all its programs on the graphics card. Apparently you haven't read the documentation. It's used to accelerate a restricted set of functions and for running programs written in C specifically for the graphics card. – Sjoerd C. de Vries May 17 '14 at 19:52
  • hmm, So is there any way to either parallelize the process or to enable graphics card utilization for front end rotation etc. – Everett Knag May 18 '14 at 00:59
  • If all is well, manually rotating a 3D plot in the FrontEnd is done by the graphics card. Calculating the plot itself, in parallel, using the GPU's processing units is not. There is no straightforward way to do this, other than writing the low-level programs to do that yourself. If you have done that CUDAlink provides tools to link that to Mathematica. – Sjoerd C. de Vries May 18 '14 at 12:02

1 Answers1

8

Perhaps you are looking for RegionPlot3D which can be used to generate the solid object you seem to want:

RegionPlot3D[
 z > Sqrt[1^2 + x^2 + y^2] && z < (Sqrt[10^2 + x^2 + y^2]), {x, -10, 
  10}, {y, -10, 10}, {z, 0, 20}, AxesLabel -> Automatic, 
 PlotStyle -> Opacity[1], PlotPoints -> 30]

Mathematica graphics

Sjoerd C. de Vries
  • 65,815
  • 14
  • 188
  • 323
  • Thank you. Now is there a way for me to find: 1. a function for the cross sectional area of the Z,y PLane at every height Z. and 2. The volume of the object. Both of these would be withing the statically bounded (x,y) region. – Everett Knag May 18 '14 at 01:03
  • Found the answer to part 2 of my question below. Too tired to think right now, but I'm sure I could derive the other equation from this discussion.http://mathematica.stackexchange.com/questions/39161/how-to-plot-and-find-the-volume-of-a-solid – Everett Knag May 18 '14 at 03:09
  • @EverettKnag "the cross sectional area of the Z,y PLane at every height Z." You mean the cross sectional area of the Z,y plane for a given x value? If not, your question is a bit mysterious. As you phrase it, you are describing a line. – Sjoerd C. de Vries May 18 '14 at 12:10
  • I apologize, that was a simple typo, I do mean the cross sectional area given on the x,y Plane. What I'm trying to do is find ,for a solid cuboid of constant density, the "amount" of mass located at every instantaneous radius from the origin. Ie, I'm trying to find dm/dr. – Everett Knag May 18 '14 at 15:03