2

How to plot a function with different colors. I want to plot the function x^3-x with distinct color. For example, using red from -1.5 to 0 and using green from 0 to 1.5. I know that I have to use PlotStylebut I don't know how write the range of the colors.

Andrea Rosero
  • 47
  • 1

3 Answers3

2
Plot[x^3 - x, {x, -1.5, 1.5}, 
 ColorFunction -> Function[{x, y}, If[x <= 0, Red, Green]], 
 ColorFunctionScaling -> False]

enter image description here

ciao
  • 25,774
  • 2
  • 58
  • 139
  • I actually have to plot this http://i.imgur.com/xAJAvf0.jpg with four different colors. I think I can do it with 2 colors, but I think I need to use different commands for 4 different colors. Thanks for your help! – Andrea Rosero May 18 '14 at 00:30
  • @AndreaRosero: Just use Switch or Which instead of the If, then you can delimit as many colors as you'd like. – ciao May 18 '14 at 00:38
  • I did this, but it doesn't seem to work http://i.imgur.com/n67ahdC.jpg – Andrea Rosero May 18 '14 at 00:48
  • Completely wrong format for Switch there, in any case Which is easier for this kind of thing: Plot[t^3 - t, {t, -1.5, 1.5}, ColorFunction -> Function[{t, d}, Which[-1.5 <= t < -1/Sqrt[3], Orange, -1/Sqrt[3] <= t < 0, Purple, 0 <= t < 1/Sqrt[3], Brown, 1/Sqrt[3] <= t < 1.5, Yellow]], ColorFunctionScaling -> False] . – ciao May 18 '14 at 01:07
  • @rasher Which switch?:) – Dr. belisarius May 19 '14 at 03:45
  • @belisarius :-) – ciao May 19 '14 at 07:33
1

One way will be to break down the plot regions as follows:

xval = {-1/Sqrt[3], 1/Sqrt[3]};
yval = Map[#^3 - # &, xval];

Show[{Plot[t^3 - t, {t, -1.5, -(1/Sqrt[3])}, 
   PlotStyle -> {Thick, Brown}], 
  Plot[t^3 - t, {t, -(1/Sqrt[3]), -(2/(3 Sqrt[3]))}, 
   PlotStyle -> {Thick, Blue}], 
  Plot[t^3 - t, {t, -(2/(3 Sqrt[3])), 1/Sqrt[3]}, 
   PlotStyle -> {Thick, Orange}], 
  Plot[t^3 - t, {t, 1/Sqrt[3], 1.5}, PlotStyle -> {Thick, Yellow}]}, 
 PlotRange -> {{-1.5, 1.5}, All}, GridLines -> {xval, yval}, 
 Ticks -> {xval, yval}, 
 GridLinesStyle -> Directive[Thickness[0.003], Magenta], 
 AspectRatio -> 1.5, 
 Epilog -> {Red, PointSize[.025], 
   Point[{-(1/Sqrt[3]), 2/(3 Sqrt[3])}], Green, PointSize[.025], 
   Point[{1/Sqrt[3], -2/(3 Sqrt[3])}], Black, 
   Text["top", {-(1/Sqrt[3]), 2.7/(3 Sqrt[3])}], 
   Text["bottom", {1/Sqrt[3], -2.7/(3 Sqrt[3])}]}]

Mathematica graphics

RunnyKine
  • 33,088
  • 3
  • 109
  • 176
1
colorPlot[fun_, lims_, colList_: {{-Infinity, Infinity}, Blue}, 
          opts : OptionsPattern[Plot]] := 
  Module[{colfun = Piecewise[{#[[2]], #[[1, 1]] < \[FormalT] < #[[1, 2]]} & /@  colList]},
   Plot[fun@t, {t, lims[[1]], lims[[2]]}, opts,
    ColorFunctionScaling -> False, 
    ColorFunction -> Function[{x, y}, colfun /. \[FormalT] :> x]]
   ];

colorPlot[Sin@# &, 
         {-1, 1},
         {{{-1, -1/2}, Blue}, {{-1/2, 1/2}, Green}, {{1/2, 1}, Red}}, 
         PlotStyle -> {Thick, Dashed}]

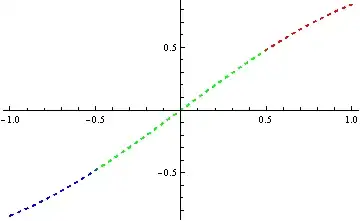
Mathematica graphics

Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453