I have a following systeme :
\begin{equation} \left\{ \begin{array}{rcr} (\beta+\frac{1}{2}\delta^{2})\nu_{1}(u)-\delta\nu_{2}(u)+\nu_{3}(u)& = &0\\ (\beta+\frac{1}{2}\delta^{2})\upsilon_{1}(u)-\delta\upsilon_{2}(u)+\upsilon_{3}(u)& < &0\\ \end{array} \right. \end{equation}
where
\begin{align*} &\nu_{1}(u)= q(u)f[q(u)],\\ &\nu_{2}(u)= f[q(u)]^2 + F(x)q(u)f[q(u)],\\ &\nu_{3}(u)= \left(u (f[q(u)])^2 + \frac{1}{2}u^2q(u)f[q(u)]\right),\\ &q[u] := Quantile[NormalDistribution[0, 1], u], \ (the \ quantale \ at \ u)\\ &f[q(u)]=PDF[NormalDistribution[0, 1], q(u)] \ (the \ density \ at \ q(u)), \end{align*}
and for the inequality, $\upsilon_{i}(u)=\nu_{i}^\prime(u)$ with respect $q(u)$ for $ i\in \{1,2,3\}$ with $(\beta,\delta,u)\in [0.1]\times[0.1]\times[0.1]$.
I would like to look at the projection of this system of equation onto the plane $(\beta,\delta)$ and $(u,\delta)$ in Mathematica or in r.
My code sets up the full 3-d view of the 3D plot, which is not what I want. And I think there are some thing wrong in my picture. I'd like to see two of the views $(\beta,\delta)$ and $(u,\delta)$ on different figure.
q[u_] := Quantile[NormalDistribution[0, 1], u]
f[x_] := PDF[NormalDistribution[0, 1], x]
h1[u_, a_, e_] := ((((a^2)/2 + e)*(-q[u])*(f[q[u]])) -
a*(-q[u]*f[q[u]]*u + f[q[u]]^2) +
u*f[q[u]]^2 - (u^2)/2*q[u]*f[q[u]])/(1/6 - a/2 + (a^2)/2 + e)
h2[u_, a_, e_] := (((a^2)/2 + e)*((q[u]^2) - 1)*f[q[u]]) -
a*(u*(q[u]^2 - 1)*f[q[u]] - 3* q[u]* f[q[u]]^2) + f[q[u]]^3 -
2*u*q[u]*f[q[u]]^2 -
u*q[u]*f[q[u]]^2 + ((u^2)/2)*(q[u]^2 - 1)*f[q[u]]
ContourPlot3D[ h1[u, a, e] == 0,
{a, 0, 1}, {u, 0.1, 0.9}, {e, 0, 1.5},
RegionFunction -> Function[{u, a, e}, h2[u, a, e] > 0]]
The graph 3D :

I want to try do verify if my plot 3D is true and if it is possible to have the projection on both plan $(\beta,\delta)$ and $(u,\delta)$.
Any thoughts on the best way to do this?
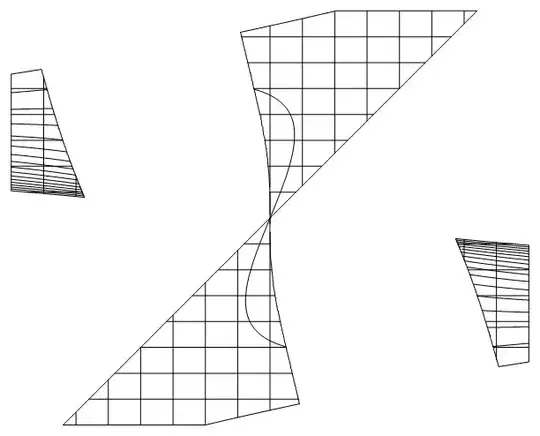


u=0. And it could be drawn in usualContourPlotAdditionally, you can see projections at your 3D graph just using appropriate
– Rom38 May 19 '14 at 22:34ViewPointViewPointhelps you to see it – Rom38 May 19 '14 at 23:09