I was trying to evaluate the following expression:
RegionPlot[a > 0 && 2 a + b == 0, {a, -2, 2}, {b, -1.5, 1},
PlotLegends -> "Expressions"]
The output is:
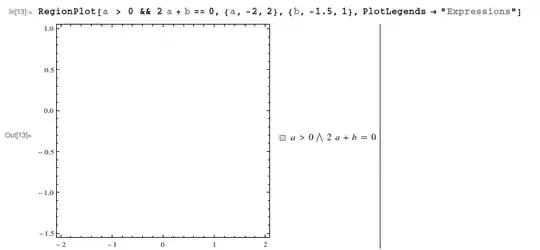
I think this is unexpected. Think about when $a = 0.5$. So, $b = -1$ which is within the range $[-1.5, 1]$. So, this values and other such values should be in a gray region in the plot. But they are not there. Any help?

?RegionPlot, The predicate pred can be any logical combination of inequalities. However, this won't work either:RegionPlot[ a > 0 && 2 a + b <= 0 && 2 a + b >= 0, {a, -5, 5}, {b, -5, 5}]I guess there must be a "true" region (with non null area), because RegionPlot initially evaluates pred at a grid of equally spaced sample points specified by PlotPoints. Then it uses an adaptive algorithm to subdivide at most MaxRecursion times, attempting to find the boundaries of all regions in which pred is True. – May 25 '14 at 17:31ContourPlotof2 a + b == 0withRegionFunction -> Function[{a, b}, a > 0]. – May 25 '14 at 17:40