6

If I have a function, f[a, b, c, d], with a, b, c and d varying between 0 and 1 continuously. What would be the best way to explore this function visually with Mathematica? Is evaluating multiple Plot3D expressions with two of the four arguments held constant my only option?

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
Sulli
  • 2,185
  • 14
  • 28

3 Answers3

12

For example:

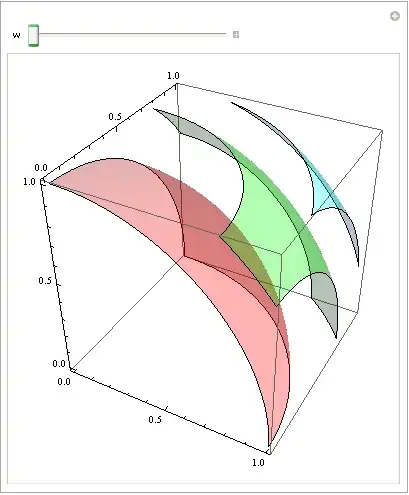
Manipulate[
 ContourPlot3D[Norm[{x, y, z}]^ (3 + w), 
               {x, 0, 1}, {y, 0, 1}, {z, 0, 1}, 
               ContourStyle -> (Directive[Opacity[.3, #]] & /@ {Red, Green, Cyan}),
               Contours -> {1, 2, 3}, MeshStyle -> None], 
{w, 0, 1}]

Mathematica graphics

Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453
  • Nice!!! Further examples plus mathematical proofs can be found in the last 3 chapters of link – eldo May 28 '14 at 18:19
  • I'm having difficulties interpreting the contour surfaces in this plot. What do they represent exactly? How can I get a feeling of how my function behaves from the contour surfaces? – Sulli Jun 02 '14 at 14:34
  • @su1 "get a feeling" is quite vague :) What exactly do you want to explore? – Dr. belisarius Jun 02 '14 at 14:45
  • for example understand from the contour surfaces how my output varies when x increases, knowing all other inputs are fixed. Basically I don't really know how to read a ContourPlot3D. It's easier to read it when it's in the form ContourPlot3D[f==g, ...] but when in the form of ContourPlot3D[f, ...] I don't know what the plot represents – Sulli Jun 02 '14 at 15:16
  • @su1 In the form I used the function you've three contours: On the red one the function value is 1, on the green one the value of the function is 2 and in the cyan contour the function evaluates to 3.Is it clear now? – Dr. belisarius Jun 02 '14 at 15:20
  • Yes it's clear. What about when you don't specify the Contours? What surface is plotted by default? – Sulli Jun 03 '14 at 07:55
  • @su1 http://reference.wolfram.com/mathematica/ref/Contours.html – Dr. belisarius Jun 03 '14 at 13:07
4

Manipulate is a great tool anyway:

Manipulate[
 ContourPlot3D[
  c - Sin[d] - a x^2 - b y^2 + z^2 == x y z, {x, -2, 2}, {y, -2, 
   2}, {z, -2, 2}, Mesh -> None, 
  ColorFunction -> Function[{x, y, z}, Hue[z]], 
  ContourStyle -> Opacity[0.75]], {a, 0, 1}, {b, 0, 1}, {c, 0, 1}, {d,
   0, 1}]

enter image description here

  • 2
    If I'm not mistaken, what you're visualizing there is a function of seven arguments. –  May 28 '14 at 22:58
0

The method you mention, using the Plot3D expressions, may be implemented pair-wise. That is: represent twin spaces (a,b,f) and (c,d,f), display the fixed values (a1,b1,0) and (c1,d1,0), and the functions f(a,b,c1,d1) and f(a1,b1,c,d), in their corresponding space. Next step, treat the "fixed" values as slider ("pilot") values, and plot the corresponding functions accordingly, letting them evolve "in real time" with their "pilot" values. I've done this with another tool, see Youtube demo at https://www.youtube.com/watch?v=s_h8tlTxRos

Guido 'wugi' Wuyts
  • 1
  • 1