6

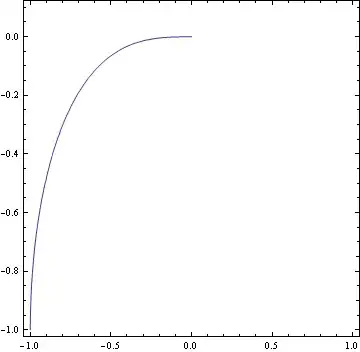
I have a problem with finding the function that gives the boundary curve in RegionPlot comamnd. I use the following code to make the regions in which two inequalities are held simultaneously 

RegionPlot[{{x^3 - y^2 > 2 y && x^2 + y^3 > 2 x }, 
            {x^3 - y^2 < 2 y && x^2 + y^3 > 2 x }}, {x, -1, 1}, {y, -1, .1}, 
           PlotStyle -> {Green, Yellow}, BoundaryStyle -> {Black, Thick}]

enter image description here

Here we see a black thick curve between the green and yellow regions, I mean the boundary that separates these regions (I showed it with a red arrow) .

Now, how can I find its equation or at least the list of points living on this curve?

Kuba
  • 136,707
  • 13
  • 279
  • 740
user14750
  • 303
  • 1
  • 5

3 Answers3

5

The "canonical" way is to find a pattern (here, {Black, Thick}) that matches what the boundary is made of and extract it from the graphics object. So given

pt = RegionPlot[{{x^3 - y^2 > 2 y && 
     x^2 + y^3 > 2 x}, {x^3 - y^2 < 2 y && x^2 + y^3 > 2 x}}, {x, -1, 
   1}, {y, -1, .1}, PlotStyle -> {Green, Yellow}, 
  BoundaryStyle -> {Black, Thick}];

bdy=Cases[Normal@First@pt, {Black, Thick, __}, Infinity];

Graphics[bdy]

enter image description here

---EDIT 2---

In diagonally reading your question, I missed the requirement for the boundary between the two.

The following will work on the particular dataset. First, you can extract the points from the bdy:

points = Cases[bdy, Line[a___] -> a, Infinity]

and you will notice that there are two components each corresponding to one region. I thought that Intersection wouldn't work for the two but as @eldo points out, it turns out it does: 

bdy = First /@ GatherBy[Intersection@@points, First] (* so that there are no duplicate x coords*);

gives the boundary points which can be fitted to a model of your liking or interpolate or whatever:

 fit = Interpolation[bdy, InterpolationOrder -> 1];

Plot[fit[x], {x, -1, 0},  
 Epilog -> {Red, PointSize -> Tiny, Point[points[[1]]~Join~points[[2]]]},
  PlotStyle -> {Blue, Thick}]

enter image description here

gpap
  • 9,707
  • 3
  • 24
  • 66
  • @gpap - Instead of working with "Nearest", couldn't one simply take the "Intersection" of the two components? – eldo Jun 04 '14 at 11:46
  • Ehmmmmmmm......I thought that wouldn't work as the points wouldn't be the same but it seems to be working fine. I think this is a bad answer as it stands so maybe I should delete alltoghether.. – gpap Jun 04 '14 at 11:49
  • please leave your answer since it's instructive, esp. the "Nearest"-function which I didn't know so far. Maybe you could make an addendum with "Intersection". - superseded, thanks gpap :) – eldo Jun 04 '14 at 12:01
4
ContourPlot[x^3 - y^2 == 2 y, {x, -1, 1}, {y, -1, .1},
            RegionFunction -> (#^2 + #2^3 > 2 # &)]

enter image description here

The following procedure contains additional condition which you've provided by range for RegionPlot: {x, -1, 1}, {y, -1, .1}.

Reduce[x^3 - y^2 == 2 y && x^2 + y^3 > 2 x && Abs[x] <= 1 && -1 <= y <= .1, 
       {x, y}, Reals]

-1. <= x < 0 && y == -1. + Sqrt[1. + x^3]
Kuba
  • 136,707
  • 13
  • 279
  • 740
2

Looking at the FullForm of

rp = RegionPlot[{{x^3 - y^2 > 2 y && 
      x^2 + y^3 > 2 x}, {x^3 - y^2 < 2 y && x^2 + y^3 > 2 x}}, {x, -1,
     1}, {y, -1, .1}, PlotStyle -> {Green, Yellow}, 
   BoundaryStyle -> {Black, Thick}];

with

rp // FullForm

you can easily see that

q = rp[[1, 1]]

and

p = First@Last@rp[[1]][[2]][[2]][[1]]

yielding

pointsoncurve = q[[p]]

Now,

ListPlot[pointsoncurve, Joined -> True, AspectRatio -> 1, 
 GridLines -> Automatic]

shows

enter image description here

It wouldn't be too difficult to "automate" this, esp. the finding of "p".

eldo
  • 67,911
  • 5
  • 60
  • 168
  • Of course, Kuba's answer is the right one here, but I leave mine in case the OP wants to see the list of points MM uses to draw the boundaries. – eldo Jun 04 '14 at 10:23
  • Well, I've not provided the list of points so it's ok. The problem is that OP wants only the part of the border that separates both regions and here's more than that. – Kuba Jun 04 '14 at 10:26