Create a matrix of matrices using Band and ArrayFlatten

Question

I can easily write a simple Band matrix using:

SparseArray[{Band[{2, 1}] -> a}, {Dim, Dim}]

where a is a number.

Now, I would use the same method to build a block matrix, using a matrix in place of variable a. The block matrix would then be flatten with ArrayFlatten.

The line above does not work, I receive an error regarding a mismatch of dimensions.

I don't want to use something like ArrayFlatten[{{M1, M2}, {M3, M4}}], explicitly inserting each matrix, M1, M2, ..., as I expect to need bigger block matrices.

Can someone tell me how to work it out?

@kguler In fact that seems like a duplicate. Do you disagree? — Mr.Wizard, Jun 07 '14 at 13:00
@Mr.W, you are right; perhaps altroware can clarify if/why it is not. — kglr, Jun 07 '14 at 13:13
That question refers to a diagonal block matrix. However, the function Fold could be useful in a more general case. I'm doing some trials. — altroware, Jun 07 '14 at 13:15
No, I don't think this helps. I need something like Band. In am not interested in the diagonal but in the lower (upper) digonal band. — altroware, Jun 07 '14 at 13:27

score 5 · Answer 1 · edited Apr 13 '17 at 12:55

Update: With a loose interpretation of the comment by the OP

I need something like Band. In am not interested in the diagonal but in the lower (upper) diagonal band.

the following simple modification of this answer gives

a "pseudo-lower-diagonal band" starting from position {2,1}:

SparseArray[Band[{2, 1}] -> matrices] // Normal // MatrixForm

enter image description here

and a "pseudo-upper-diagonal band" starting from position {1,3}:

SparseArray[Band[{1, 3}] -> matrices] // Normal // MatrixForm

enter image description here

Original post:

Perhaps something like the following is what you need:

You have a number of matrices, say four of them, a, b, c, d (styled for later use):

matrices = {Array[Style[Subscript[a, #1, #2], Red, Bold, 16] &, {2, 3}], 
   Array[Style[Subscript[b, #1, #2], Blue, Bold, 16] &, {3, 2}], 
   Array[Style[Subscript[c, #1, #2], Green, Bold, 16] &, {2, 2}], 
   Array[Style[Subscript[d, #1, #2], Orange, Bold, 16] &, {3, 3}]};
MatrixForm /@ matrices

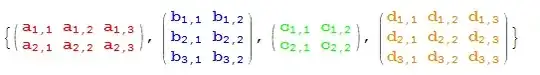
enter image description here

and the same number of starting positions

starts = RandomInteger[{1, 10}, {4, 2}] (* ignoring the possible overlaps *)
(* {{3,3},{10,3},{7,9},{6,7}} *)

and you want to place the matrices in a sparse array with the above starting positions:

sa = SparseArray[Band[#] -> #2 & @@@ Transpose[{starts, matrices}]];

This is what sa looks like:

sa // Normal // MatrixForm

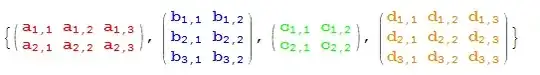
enter image description here

Yes, your interpretation was right.It is great, Band can still be used with block matrices, but we have to give the whole sequence of matrices {a,a,...} instead of just a. — altroware, Jun 09 '14 at 00:46

score 5 · Accepted Answer · answered Jun 07 '14 at 17:14

It looks to me like you need KroneckerProduct. I'll define all matrices as SparseArray below, with the band matrix having only 1s on the off-diagonal. Then KroneckerProduct inserts the desired matrix insertMatrix where the 1 appeared in the original matrix. The result is also a SparseMatrix, so I apply Normal to show the final structure:

baseMatrix = SparseArray[{Band[{2, 1}] -> 1}, {4, 4}];

insertMatrix = SparseArray@Array[Subscript[a, ##] &, {4, 2}];

blockMatrix = KroneckerProduct[baseMatrix, insertMatrix];

Normal[blockMatrix] // MatrixForm

matrix

You can generalize this by constructing a more complicated matrix as a sum of KroneckerProducts.

Create a matrix of matrices using Band and ArrayFlatten

2 Answers2

Linked