3

I'm Trying to use Mathematica to symbolically integrate a function with respect to x, y, and z.

For some reason, this computation either takes about, 60s and returns the input, or takes many hours and doesn't seem to finish. here is a screenshot of the problem. This is an attempt to integrate the gravitational potential equation over x, y, and z. The constants have been pulled out of the integration in order to try and reduce computation error or time.

integration of gravitational force

as you can see, at this moment in time, mathematica has been working for over 20,000 seconds (running about 30% on i7 @ 2.8ghz.

I feel like perhaps there is an error in my formatting, because i've run into many problems attempting to perform similar integration. I've used assumptions in past attempts, but they've haven't proved useful.

any suggestions?

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Everett Knag
  • 63
  • 3
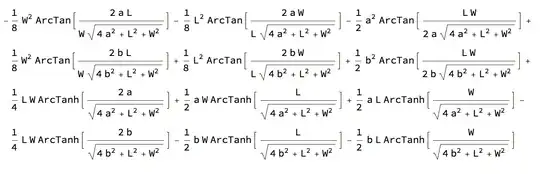
  • It will likely help to specify Assumptions->{L>0,W>0,a>0,b>a} etc (or whatever they should be ) – george2079 Jun 10 '14 at 20:36
  • You can use Integrate[1/Sqrt[x^2 + y^2 + z^2], x, y, z], as this does quickly give an answer. Then fill in the bounds manually. – Jacob Akkerboom Jun 10 '14 at 20:37
  • Can I fill them in manually? How can I fill in the x-bounds if it has then been integrated dy. Should I do this one step at a time? Is there a reason why adding bounds is so hard for Mathematica? – Everett Knag Jun 10 '14 at 20:42
  • @JacobAkkerboom I'm not sure what to do with that multiple indefinite either - may be a useful answer if you can show the steps.. – george2079 Jun 10 '14 at 20:49
  • The definite form does work with assumptions.. (add z>0 as well ). The result is such a mess that you may as well just do it numerically though. – george2079 Jun 10 '14 at 20:59
  • 3
    One thing that sometimes "works" is to assign to the positive parameters various mathematica constants. Could in this case do, say,Integrate[-1/Sqrt[x^2 + y^2 + z^2], {z, Catalan, EulerGamma}, {x, 0, Khinchin}, {y, 0, Glaisher}] // AbsoluteTiming. After which you can substitute with {Catalan->a, EulerGamma->b, Khinchin->L/2,Glaisher->W/2}. – Daniel Lichtblau Jun 10 '14 at 22:21
  • 1
    Interesting trick! - it is marginally faster in this case. You need to be wary of conditions on the parameters that might get missed by feeding specific values though. – george2079 Jun 11 '14 at 14:58
  • 1
    What is the ShowProgress function code? It very interesting. – Mariusz Iwaniuk Mar 29 '18 at 18:36
  • @MariuszIwaniuk Not sure if these give the same code the OP's using, but you might want to take a look at: https://mathematica.stackexchange.com/questions/5978/how-to-create-a-progress-bar/5980#5980 – theorist Jul 15 '18 at 03:54

2 Answers2

6

since I claimed it worked here is what i did:

 xy = Integrate[ -1/Sqrt[x^2 + y^2 + z^2] , {x, 0, L/2}, {y, 0, W/2},
    Assumptions -> {L > 0, W > 0 , z > 0, a > 0, b > a}];
 Integrate[ xy , {z, a, b}, 
        Assumptions -> {L > 0, W > 0 , z > 0, a > 0, b > a}]

result a page full of Logs and ArcTans and a few ConditionalExpressions

The full triple integral is taking way longer than the two stage approach for some reason.

Edit.. finally finished ( I also changed the integration order and added b>0)

 Integrate[ -1/Sqrt[x^2 + y^2 + z^2] , {z, a, b},
       {x, 0, L/2}, {y, 0, W/2},
         Assumptions -> {L > 0, W > 0 , z > 0, a > 0, b > 0 , b > a}] // AbsoluteTiming

enter image description here

per Michael's comment after FullSimplify

enter image description here

george2079
  • 38,913
  • 1
  • 43
  • 110
5

Using the Rubi integration package for Mathematica (http://www.apmaths.uwo.ca/~arich/), this takes under three seconds on a late-2014 MacBook Pro, requires no assumptions, and gives a relatively clean result:

x1 = Int[-1/Sqrt[x^2 + y^2 + z^2], x];
x2 = (x1 /. x -> L/2) - (x1 /. x -> 0);
y1 = Int[x2, y];
y2 = (y1 /. y -> W/2) - (y1 /. y -> 0);
z1 = Int[y2, z];
z2 = (z1 /. z -> b) - (z1 /. z -> a)

[Rubi doesn't do definite integrals, which is why I had to add separate statements (x2, y2, and z2) to compute those.]

enter image description here

AbsoluteTiming for the entire cell was 2.4 s.

theorist
  • 3,633
  • 1
  • 15
  • 27