8

I would like to mesh the surface of a cloud of points that may not be completely convex, for example the points in this question. Mathematica does not provide triangulation of 3D points, but there is a link to TetGen

 Needs["TetGenLink`"]

 {mypts, mysurface} = TetGenConvexHull[dat];
 Graphics3D[GraphicsComplex[mypts, Polygon[mysurface]], Boxed -> False]

which results in this

enter image description here

Notice it doesn't get the surface meshing associated with subtle twist in the curved shape, and meshes points further away in the goal of creating a convex object. I suppose one could try to mesh the surface piece by piece and slowly merge it as in this answer, but that sounds like a nightmare.

Here is the cloud of points for reference:

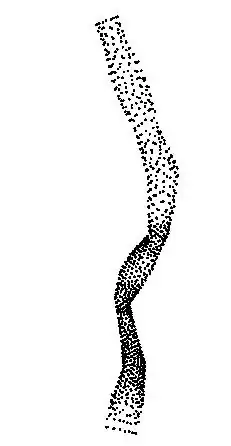
enter image description here

Community
  • 1
lalmei
  • 3,332
  • 18
  • 26
  • @Öskå I asked myself the same question today lol, then decided to play around with it. – lalmei Jun 13 '14 at 18:28
  • Oh I'm sorry I didn't check the beginning of the question :) Deleting comments! – Öskå Jun 13 '14 at 18:33
  • One can easily get that – Öskå Jun 13 '14 at 18:38
  • @Öskå Does it contain the surface polygons ? If that is the case that is what I need. – lalmei Jun 13 '14 at 18:41
  • Generally, ListSurfacePlot3D can do this. However, it won't work well for this particular point cloud. It will work for the other, straight tube that he posted. Representing a surface as a list of points is not precise, and it's generally not a good idea. For example: where are the holes in the surface? However, in some cases this is the only (experimental) data one has. – Szabolcs Jun 13 '14 at 18:57
  • I don't think it does, it is, as Szabolcs pointed, made with ListSurfacePlot3D. – Öskå Jun 13 '14 at 19:30
  • @Szabolcs representing a surface as a list of points should be fine. And generally that is how most 3D models are build, we usually push them through a 3D-delaunay triangulator and pick the surface polygons. The software that I have used in the past usually has options for convex or not-convex (concave). This is usually done on a surface you have a high sampling to avoid exactly what you mentioned, missing some important topological feature. I think TetGen actually has this capability but doesn't seem to be included with the link, but I could be mistaken – lalmei Jun 13 '14 at 21:02
  • @Szabolcs Actually given belisarius's answer I might try to redo this with matlab delaunay using your MATLink, since I think it might be a bit faster. But I will need to double check. – lalmei Jun 13 '14 at 21:06
  • @lalmei If you solve it with MATLink/MATLAB, drop me a mail. I'm curious. – Szabolcs Jun 13 '14 at 21:22
  • Can you repost the data on pastebin, the link above seems dead. I'm trying to write a solution with the functions introduced in V10. – RunnyKine Jul 27 '14 at 17:27
  • @RunnyKine that wasn't my question I linked to. – lalmei Aug 01 '14 at 09:34

1 Answers1

10

Using Simon's answer (all credit to him):

Needs["TetGenLink`"]
file = "https://dl.dropboxusercontent.com/u/68983831/curved_pipe02.txt";
dat = Import[file, "Table"];
{pts, tetrahedra} = TetGenDelaunay[dat];
csr[{aa_, bb_, cc_, dd_}] := 
 With[{a = aa - dd, b = bb - dd, c = cc - dd}, 
  Norm[a.a Cross[b, c] + b.b Cross[c, a] + 
     c.c Cross[a, b]]/(2 Norm[a.Cross[b, c]])]
radii = csr[pts[[#]]] & /@ tetrahedra;
alphashape[rmax_] := Pick[tetrahedra, radii, r_ /; r < rmax]
faces[tetras_] := 
 Flatten[tetras /. {a_, b_, c_, 
     d_} :> {{a, b, c}, {a, b, d}, {a, c, d}, {b, c, d}}, 1]
externalfaces[faces_] := 
 Cases[Tally[Sort /@ faces], {face_, 1} :> face]
polys = externalfaces@faces@alphashape[.001];
Graphics3D[GraphicsComplex[pts, Polygon@polys], Boxed -> False]

polys = externalfaces@faces@alphashape[.001];
Graphics3D[GraphicsComplex[pts, Polygon@polys], Boxed -> False]

Mathematica graphics

Community
  • 1
Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453