Why will Mathematica not give a soluion to Solve[Log[x] == Log[j, Log[j, x]], j], but Wolfram Alpha will?
Asked
Active
Viewed 582 times
3
martin
- 8,678
- 4
- 23
- 70
1 Answers
5
Wolfram|Alpha points out that this is a solution over the reals:
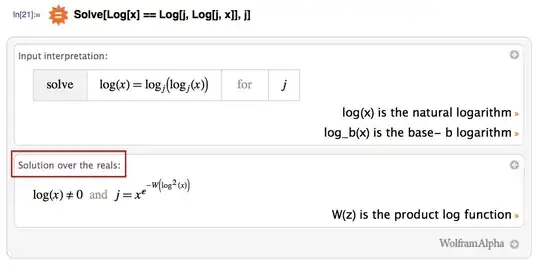
This is how to get this solution in Mathematica:
Reduce[Log[x] == Log[j, Log[j, x]], j, Reals]
(* Log[x] != 0 && j == x^E^-ProductLog[Log[x]^2] *)
Wolfram|Alpha tries to interpret input as natural language. Certain Mathematica expressions work, but they don't always do the same thing as in Mathematica. Here W|A interprets the input as "solve this equation with reasonable assumptions", not as "run the Mathematica code Solve[Log[x] == Log[j, Log[j, x]], j]".
Szabolcs
- 234,956
- 30
- 623
- 1,263
-
-
-
... Is there any way of solving for an extra
Log? ieReduce[Log[x] == Log[j, Log[j, Log[j, x]]], j, Reals]? – martin Jun 16 '14 at 14:16 -
1@martin
Solvetends to be faster because it doesn't seek a general solution. E.g. in v8Solve[Sin[x] == y, x]returned{{x -> ArcSin[y]}}which is not the general solution.Reduce[Sin[x] == y, x]returnedC[1] \[Element] Integers && (x == \[Pi] - ArcSin[y] + 2 \[Pi] C[1] || x == ArcSin[y] + 2 \[Pi] C[1])which is general. I couldn't find a v9 example off the top of my head but that's the main difference. In v9 (?)Solvecan take the optionMethod -> Reduceto do whatReducedoes ... (check the docs for another example on this). – Szabolcs Jun 16 '14 at 14:16 -
Reduceworks. – Michael E2 Jun 16 '14 at 14:04Reduce[Log[x] == Log[j, Log[j, x]], j, Reals]. In general, you should not assume that Mathematica commands typed into WolframAlpha will be executed verbatim on the server side. – Mark McClure Jun 16 '14 at 14:05Solve[Log[x] == Log[j, Log[j, x]], j, Reals, Method -> Reduce], an option which I had forgotten. – Michael E2 Jun 16 '14 at 15:44