Maximum of Minimum of a two variable function

Question

I have

F[x, y] := (y/2)(2 Cos[2x] + 2 Cos[x] + 1)/5 + ((1 - y)/2)(2 Cos[x] + 1)/3.

I am looking for the maximum of the minimum of F.

More precisely I am looking for

$$\underset{0\leq y\leq 1}{Maximum} \left(\underset{x\in [0,2\pi]}{Minimum} F(x,y)\right).$$

I typed Findminimum / FindMaximum together into Mathematica, but that did not work. I now feel that I need more advanced tools to make it work. The answer for my example is -1/9.

FindMinimum et al. probably not useful to you for this: They are for finding local min/max. You could try solving for critical points, then sieve them, or get sneaky and abuse plot/mesh functions to extract them. See e.g. here (and other tricks in other answers there). — ciao, Jun 17 '14 at 06:39
What precisely does that notation mean? Is it "minimize F over {0-2Pi,0-1}, then hold the corresponding value of x constant and find the y that maximizes F for that x, and return F(x,y)"? — mfvonh, Jun 17 '14 at 07:02

score 7 · Answer 1 · answered Jun 17 '14 at 10:02

As per rasher's suggestions:

Finding critical points:

f[x_, y_] := (y/2) (2 Cos[2 x] + 2 Cos[x] + 1)/
    5 + ((1 - y)/2) (2 Cos[x] + 1)/3.
Solve[{D[f[x, y], x] == 0, D[f[x, y], y] == 0}, {x, y}]

yields:

{{x -> 0.}, {x -> -2.30052, y -> 0.5}, {x -> 2.30052, y -> 0.5}}

Note (i) this does not find all solutions (note symmetries of surface) (ii) the third (and symmetrical solution around Pi) are in the domain of interest (iii) the third solution is a saddle point (see following):

g[a_, b_] := 
 D[f[x, y], {x, 2}] D[f[x, y], {y, 2}] - 
   D[f[x, y], x, y]^2 /. {x -> a, y -> b}
g[2.300523983021863`, 0.5]
g[2Pi-2.300523983021863`, 0.5]

both yield: -0.246914 <0 -> saddle point

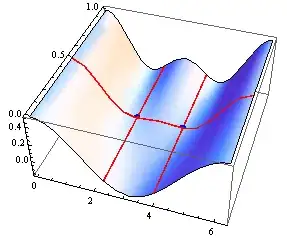
Displaying surface at y=1/2 shows symmetry (with some cheating with Mesh):

Plot[f[x, 1/2], {x, 0, 2 Pi}, MeshFunctions -> {#2 + 1./18.01 &}, 
 Mesh -> {{0}}, PlotRange -> {-0.2, 0.5}, 
 MeshStyle -> PointSize[0.03], PlotPoints -> 200]

enter image description here

The intersection shows the saddle points:

Show[Plot3D[Evaluate@f[x, y], {x, 0, 2 Pi}, {y, 0, 1}, 
  MeshFunctions -> {#1 &, #2 &}, 
  Mesh -> {{2 Pi - 2.300523983021863`, 2.300523983021863`}, {0.5}}, 
  MeshStyle -> {{Red, Thickness[0.006]}}], 
 Graphics3D[{Blue, PointSize[0.03], 
   Point[{##, f[##]} & @@@ {{2 Pi - 2.300523983021863`, 
       0.5}, {2.300523983021863`, 0.5}}]}]]

enter image description here

score 4 · Answer 2 · answered Jun 17 '14 at 07:28

I find a different solution.

f[x_, y_] = TrigExpand[(y/2) (2 Cos[2 x] + 2 Cos[x] + 1)/5 + ((1 - y)/2) (2 Cos[x] + 1)/3]  
            /. Sin[z_]^2 -> 1 - Cos[z]^2
(* 1/6 - y/15 + Cos[x]/3 - 2/15 y Cos[x] + 1/5 y Cos[x]^2 - 1/5 y (1 - Cos[x]^2) *)

min = Minimize[{f[x, y] /. Cos[x] -> cos, 0 <= y <= 1, -1 <= cos <= 1}, cos]

Maximize[{min[[1]], 0 <= y <= 1}, y] 
(* {-(1/18), {y -> 1/2}} *)

Maximum of Minimum of a two variable function

2 Answers2