I would like to examine percolation on a random lattice. To be exact, I wish to find the minimum length of a 'bond' needed such that the leftmost site can be connected to the rightmost site.
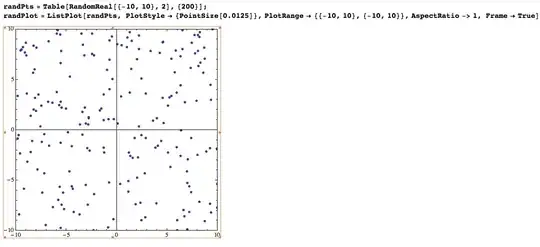
Here is an example of the lattice:
randPts = Table[RandomReal[{-10, 10}, 2], {200}];
randPlot = ListPlot[randPts,
PlotStyle -> {PointSize[0.0125]},
PlotRange -> {{-10, 10}, {-10, 10}},
AspectRatio -> 1,
Frame -> True]
I have tried for a while to get this but have not had success. The basic plan was:
Define a bond length $R$
Look at each site one at a time. If another site(s) is within $R$ of a site, they will be in the same cluster. Each site will be in a cluster of 1 or more (obviously the larger $R$ chosen, the larger each cluster size)
Take a site. Does it bond with other sites? If so then combine the two clusters together.
Repeat step 3 for all sites.
At the end ask if the leftmost cite and the rightmost sites are included in the conglomerate cluster. If so, percolation has occurred.
Decrease $R$ and start over again until a threshold is found.
I think I am stuck somewhere in the step 3,4 area.
Here is some of what I've tried:
I have defined a module to find the distance between a site, j, and its nearest neighbor. The table, t, gives distance between j and all other sites:
minD[j_] :=
Module[{},
t = Table[{randPts[[i]],
Sqrt[(randPts[[j, 1]] - randPts[[i, 1]])^2 + (randPts[[j, 2]] -
randPts[[i, 2]])^2]},
{i, 1, Length[randPts]}];
For[i = 1, i < Length[t] + 1, i++,
If[t[[i, 2]] == RankedMin[t[[All, 2]], 2],
coord[j] = t[[i, 1]] ]];
Return[{coord[j]}];
];
This module takes the table of distances and picks out ones that are within the chosen bonding radius (1.5 here. the y>0 condition to so to not count the same site):
cluster[k_] :=
Module[{},
minD[k];
Return[
Table[Cases[t, {x_, y_} /; y < 1.5 && y > 0][[i]][[1]],
{i, 1, Length[Cases[t, {x_, y_} /; y < 1.5 && y > 0]]}]];
]
So cluster[k] gives the sites within the cluster that is centered at site k.
Now combining these clusters is what I am having a problem with. My idea was to start with a site and its cluster; find out what clusters that cluster intersects with and continue. I was not able to implement this correctly.
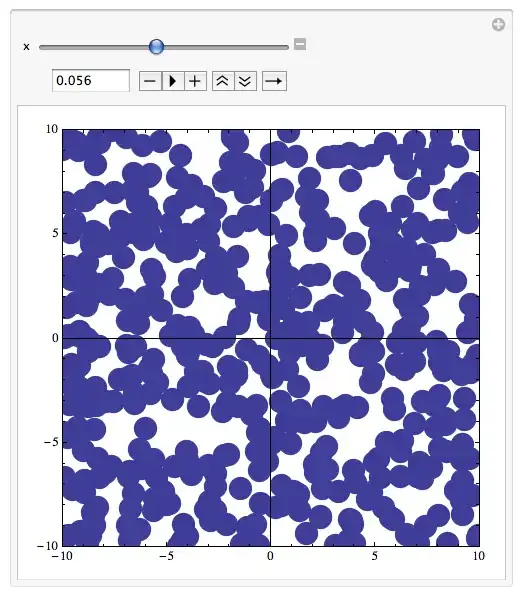
Another way to visualize or maybe solve the problem is in terms of increasing the site radius at each site until a percolation network is achieved:
randMovie =
Manipulate[
ListPlot[randPts,
PlotStyle -> {PointSize[x]},
PlotRange -> {{-10, 10}, {-10, 10}}, AspectRatio -> 1,
Frame -> True],
{x, 0.00, 0.12, 0.002}]





randPtscan be writtenRandomReal[{-10, 10}, {200, 2}]– Mr.Wizard May 04 '12 at 22:53Returnis not really returning values from aModule. Instead of usingModule[{}, ...; Return[result]; ]simply useModule[{}, ...; result](not that lack of the final semicolon). In general, you almost never need to useReturnin Mathematica, and when you do, it's good to be aware of some unusual behaviour ... – Szabolcs May 05 '12 at 09:49