Getting good-looking matrix form output from a matrix having both scalars and matrices as elements

Question

I have a nested matrix n:

n = {{a, b}, {c, d}}
a = {{0, t, q, dh}, {0, 1, 0, th}, {1, 1, 0, sh}}
b = {{0, t, q, dh}, {1, 0, 0, th}, {1, 0, 0, sh}}

c = {{0, t, q, dh}, {0, 1, 0, th}, {1, 0, 0, sh}}
d = {{0, t, q, dh}, {0, 0, 0, th}, {0, 1, 0, sh}}

With thanks to Nasser add column and Andy and Mike most efficient for their questions and answers, we can add a vector m = {rr, kk} to this nested matrix as a column, for example:

pp = Transpose[Insert[Transpose[n], Flatten@m, 1]]
or
pp=Join[List /@ m, n, 2] // MatrixForm

Finally, after running the above lines we have pp as:

{{rr, {{0, t, q, dh}, {0, 1, 0, th}, {1, 1, 0, sh}},       
      {{0, t, q, dh}, {1, 0, 0, th}, {1, 0, 0, sh}}}, 
 {kk, {{0, t, q, dh}, {0, 1,0, th}, {1, 0, 0, sh}}, 
      {{0, t, q, dh}, {0, 0, 0, th}, {0, 1, 0,sh}}}}

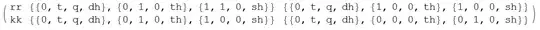
and pp/MatrixForm as: enter image description here

The result is correct but I wanted to obtain an obvious and clarified figure of pp/MatrixForm same as :

enter image description here

Are there any possibility for obtaining the last form instead of the first form for pp/MatrixForm.

Thank you so much, It was wonderful. I am so sorry can I ask a question,is the role of {2;;} for existence of 2 rows? for example if I had pp 3 rows I must write {3;;}? — Unbelievable, Jun 27 '14 at 04:46
I posted a cleaner version using MapAt which should work regardless of the numbers of rows/columns. — kglr, Jun 27 '14 at 04:52

score 3 · Answer 1 · answered Jun 27 '14 at 04:34

Let's define your matrix as

p = {{rr, {{0, t, q, dh}, {0, 1, 0, th}, {1, 1, 0, sh}},       
  {{0, t, q, dh}, {1, 0, 0, th}, {1, 0, 0, sh}}}, 
  {kk, {{0, t, q, dh}, {0, 1,0, th}, {1, 0, 0, sh}}, 
  {{0, t, q, dh}, {0, 0, 0, th}, {0, 1, 0,sh}}}};

You could do the MatrixForm on the outermost and the inner levels:

#[Map[#,p,{2}]]&@MatrixForm

MATRIX

An alternative form would be

MatrixForm//#[Map[#,p,{2}]]&

score 3 · Accepted Answer · answered Jun 27 '14 at 04:47

3

pp = {{rr, {{0, t, q, dh}, {0, 1, 0, th}, {1, 1, 0, sh}},       
          {{0, t, q, dh}, {1, 0, 0, th}, {1, 0, 0, sh}}}, 
     {kk, {{0, t, q, dh}, {0, 1,0, th}, {1, 0, 0, sh}}, 
          {{0, t, q, dh}, {0, 0, 0, th}, {0, 1, 0,sh}}}}; 

MapAt[MatrixForm, pp, {{All, All}, {}}]

enter image description here

answered Jun 27 '14 at 04:47

kglr

394,356
18
477
896

Inasmuch as, I need so much to do work with matrices, are there any comprehensive documents for the matrices category and some related syntax, like Map, Mapat, MapThread and so on? because the help of Mathematica is not enough for being expert in this territory. – Unbelievable Jun 27 '14 at 05:14
@mostafa, I find the tutorials in Virtual Book extremely useful. – kglr Jun 27 '14 at 05:51

Getting good-looking matrix form output from a matrix having both scalars and matrices as elements

2 Answers2

Linked