Why are functions called first-class objects in Mathematica?

Question

I've heard lots of people say a function is a first-class object in Mathematica. "Everything is an expression, including function." "There is no distinction between functions and data."

Having read the book Power programming with Mathematica up to Chapter 5, I think I already have some basic knowledge about Mathematica, but I'm still confused with this point.

To be more specific, I think there is a critical difference between functions and data. When we treat f as a function, we would use f[3] (must use the brackets); whereas to have f treated as a usual expression, we would simply use f. So I think a function (such as f[x_] := x^2) and data/expression (such as f := x^2 or f = 123) are totally different! A function can accept several arguments, but a normal expression can not! "There's no difference between functions and data", is it real?

I also have another question (which has nothing to do with above). If we let symbol f have two characters "function" and "data(expression)" in the meantime, there will cause some problem.

1.

ClearAll[f]
f = 9
f[x_]:=x^2 (* message is printed *)

2.

ClearAll[f]
f[x_]:= x^2
f = 9   (* MMA considers it is legal here *)
?f      ( *MMA shows the two definition of f above, but f is no longer 
          related to squaring something, as we can see below. *)
f[100]  (* this returns 9[100] *)
f       (* this returns 9 *)

Why is 2 OK, but not 1? In case 2, why does Mathematica not erase the definition of "function" f when we define f = 9? Furthermore, why does Mathematica allow the apparent error syntax 9[100] without giving an error message? (We are very certain about numbers must not be a function name, the head of an normal expression!)

Answer 1

I'm guessing you're coming from a programming language where every expression must evaluate to a value, and if it didn't evaluate to something (like 5[Cos+Sin]), it's a syntax error. To me, Mathematica started to make a lot more sense, once I stopped thinking about functions and values, and started to think of every expression as evaluating to an "expression tree". (Note to long-time Mathematica users: I'm trying to explain this form the point of view of someone coming from a different programming language. I'm glossing over a lot of details like Set vs SetDelayed, Evaluate and Hold, but the "conceptual model" I'm trying to explain here was very useful for me when I started with MMA.)

So, e.g. a+b*c yields an expression tree. You can use TreeForm[a + b*c] to display the actual tree:

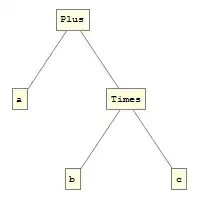
The same is true for a[b*c], or even (b*c)[a]. Think of these things as tree data structures, not as expressions as you might know them from C or Perl. For instance, you can access parts of that data structure using normal array-index syntax: (a + b*c) [[2, 1]] yields b. There are a few basic rules how operators can be combined, so e.g. a+*b or x=[b] are invalid, but other than that, you can build any tree you want.

The next step is that you can tell Mathematica tree manipulation rules that it should automatically apply to these trees. You could for example write:

a[x_ + c] := "Hello"

Now, any time Mathematica evaluates a tree that matches the pattern a[x_ + c], it will replace it with "Hello". Don't think of this as a function declaration. Think of it as a replacement rule. And you can define almost any kind of pattern matching and replacement rule. For example, you could write the replacement rules:

(x_ + b)[y_] := x*y
z_ + c := 5 z

and Mathematica would from then on happily evaluate an expression like (5+b)[6] to 30 or 5+c to 25.

(Note: Don't actually do this. It's a bad idea. In fact, it's such a bad idea that the people at Wolfram decided to protect the symbol Plus from being overwritten, to prevent you from doing this. But if you Unprotect[Plus], you could actually do this.)

Also note, that when you define a "variable":

z := 10;

you're using exactly the same machinery. (Again, ignoring details like DownValues you can think of those as ugly performance improvement tricks.) This tells Mathematica to replace any expression tree that matches the pattern z by 10. We're calling some of these patterns "functions", other "variables", but to the Mathematica kernel, there's really no difference.

(You're maybe asking yourself now: Wait, I declare variables using =, not :=, right? In the cases above, you can actually use both, with the same results. = and := are shorthands for Set and SetDelayed, respectively, which "register" a new pattern replacement rule with the Mathematica kernel. The only difference is that Set evaluates the second argument, while SetDelayed leaves it unevaluated.)

Here's another example, let's say you write:

Clear[x,f]
x = f[5]

This tells the Mathematica kernel that any expression that looks like x is to be replaced with f[5]. So if you enter x+y now, it evaluates to the expression tree y+f[5]. Mathematica doesn't care that f looks like a function to you and me - to Mathematica, this is just another old tree structure.

Now let's you set:

f[a_] := a*2

Again, this registers a new replacement rule. Now if we evaluate x+y, it (at first) evaluates to y+f[5]. But the kernel immediately notices that there's a replacement rule that matches f[5], and replaces it, with 2*5. So the expression evaluates to 10+y.

You should not think of this as "variable x changed its value". x never changed its value, it's still set to the expression tree f[5]. You can Clear[f] and evaluate x again to check.

All this is a bit confusing when you're coming from a "conventional" programming language. But it is extremely useful for manipulating symbolic expressions. For example, with the knowledge you have now, you could probably write a function that takes the derivative of a basic arithmetic expression in about 10 lines. Try that in a conventional programming language!

Answer 2

When you use the syntax f[x_]:= ... in Mathematica, you are not defining a function f. You are defining a pattern-replacement rule. The documentation and the users tend to be vague or misleading or just incorrect about this point. Of course you can define "function" as something quite to your liking and ignore the protestations of mathematicians, "functional programming" fans etc.

Here is an actual function definition in Mathematica.

f = #^2&

in FullForm it looks like this:

Function[Power[Slot[1],2]]

You can apply the function f in the usual way, e.g. f[5] returns 25.

How does this differ from what you might write, f[x_]:=x^2 ?

Consider this as a function ...

g[x_Integer]:= x^2;
g[x_Real]:=x^3

and you see it is not really a function but a set of two rules.

Now what does it meant to say that functions are first class objects?

You can use f in various ways that might not be legal in other languages. You can pass f as an argument to a function. You can use it in expressions. For example, Sin[f]. Not that it necessarily makes sense, but it is not illegal.

Since what you probably meant by Function is in Mathematica terminology a Rule, you might ask, is a Rule a first class object. Yes. Is the rule set that is associated with a name like g, above, a first class object, probably not, though this following example may play more with Mathematica's bindings than you find comfortable. Using the above definition of g..

test[fun_, k_] := Block[{g = Print[nope] &} , fun[k]]

now test[g,3] returns / prints nope.

Answer 3

The OP asks in a comment:

One more question. Clear[f, g];f = g;f[x_] = x^4, I can understand the result of ?g. However, why {g,h,j}[[1]]=6 causes error? When using =(Set), MMA first evaluate the first part f and {g,h,j}[[1]] to g and g right?(i.e. always evaluating lhs before assignment) Why is f[x_] = x^4 ok, but not {g,h,j}[[1]]=6?

The OP indicates that he now understands standard evaluation, but it would seem that he has yet to grasp non-standard evaluation. Because it has the HoldFirst attribute, Set can and does non-standard evaluation of its first argument. It expects its unevaluated first argument to be a symbol. The reason for this is that Set has side-effects. It changes the binding of the unevaluated symbol passed into it.

Consider

a = {g, h, j}; a[[1]] = 6; a

{6, h, j}

The above code not only rewrites the list {g, h, j} to {6, h, j}, it also changes the binding of a; it has no effect on g. In this code, g is just a placeholder.

The code

{g, h, j}[[1]] = 6

doesn't work because, although Set can rewrite the list {g, h, j} to {6, h, j}, it doesn't have a symbol to bind to the rewritten list. So it can't accomplish its side effect, forcing it to print a message and fail.

Note that as part of its non-standard evaluation, Set must recognize when its first argument is bound to a Part expression and treat it differently. In such a case, it must rewrite the list appropriately (maybe using ReplacePart) rather the making the simple rebinding it does with symbol bound to,say, an atom.