Other solutions are fine, but they use old MatrixConditionNumber as a magic box. However, it has a simple idea. The 2-norm condition number of the matrix $M$ is a ratio $\sigma_{\rm max}/\sigma_{\rm min}$ between the maximum and the minimum singular values. The maximum singular value $\sigma_{\rm max}$ can be estimated by a simple power iteration:
\begin{align}
u_0&={\rm random},\\
u_{i+1}&=M M^\dagger u_i/|u_i|,\quad i=1,\ldots,n-1\\
\sigma_{\rm max}^2&\approx |u_n|.
\end{align}
The minimum singular value $\sigma_{\rm min}$ can be estimated by the same power iteration with $M^{-1}$ instead of $M$, which means to solve linear system on each step. So
condNum2[m_, k_: 10] := Module[{s, u1, u2},
s = Internal`DeactivateMessages@LinearSolve@m;
{u1, u2} = RandomReal[NormalDistribution[], {2, Length@m}];
Do[
u1 = m.Conjugate[Conjugate@Normalize@u1.m];
u2 = s[s@Normalize@u2, "C"];
, {k}];
Sqrt[Norm@u1 Norm@u2]
]
SeedRandom[0];
n = 1000;
m = SparseArray[RandomInteger[{1, n}, {10 n, 2}] -> RandomComplex[1 + I, 10 n]];
condNum2[m] // AbsoluteTiming
(* {0.205369, 3599.44} *)
MatrixConditionNumber[m, 2] // AbsoluteTiming
(* {0.220560, 3599.45} *)
Here s[...,"C"] solves the conjugated transposed linear system.
Another possibility is to find the maximum and the minimum singular values by the Arnoldi algorithm
SingularValueList[m, 1, Method -> "Arnoldi"]/
SingularValueList[m, -1, Method -> {"Arnoldi", "Shift" -> 0}] // First // AbsoluteTiming
(* {0.464198, 3599.46} *)


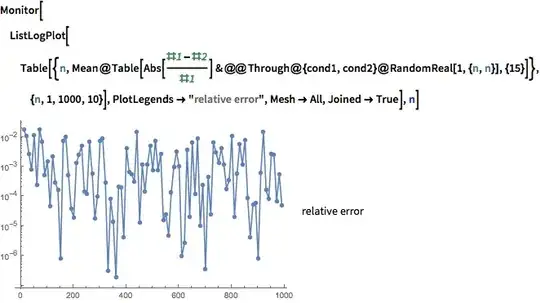
Norm[mat,2]Norm[Inverse@mat,2], but this is unsatisfying... – jtbandes Jul 17 '14 at 06:27LUDecomposition(the third part of the result is that estimate). For the 1-norm take theLUDecompositionof the transpose. – Daniel Lichtblau Jul 17 '14 at 21:47