Replace interior of matrix with zeros

Question

I have f.e. the following square matrix:

x = {{2, 5, 5, 11, 11, 23, 37, 41, 43, 47},
    {2, 5, 11, 17, 19, 23, 41, 41, 43, 67},
    {2, 7, 11, 19, 19, 41, 41, 43, 47, 73},
    {3, 11, 17, 19, 23, 41, 43, 53, 67, 79},
    {3, 11, 19, 19, 31, 43, 47, 59, 67, 83},
    {3, 17, 19, 29, 37, 43, 53, 59, 73, 83},
    {5, 17, 29, 31, 37, 47, 53, 71, 73, 83},
    {7, 19, 29, 31, 37, 53, 59, 73, 73, 89},
    {11, 23, 31, 41, 43, 53, 61, 73, 79, 97},
    {29, 29, 37, 41, 53, 67, 71, 79, 79, 97}};

I want to keep the first and last row / column and replace all other numbers with 0. I have written:

n = Length@First@x;

Table[x[[i, j]] = 0, {i, 2, n - 1}, {j, 2, n - 1}];

x // MatrixForm

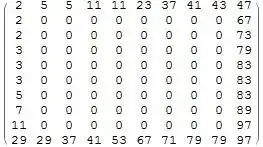
enter image description here

Before that I tried to find a more functional solution (f.e. with replacement patterns) but gave up after some unsuccesful attempts. Thanks for showing me some alternatives.

Kuba · Answer 1 · 2014-07-09T19:42:03.080

21

You can do:

x[[2 ;; -2, 2 ;; -2]] = 0;
x

or

ReplacePart[x, {i, j} -> 0 /; And @@ MapThread[Less, {{1, 1}, {i, j}, Dimensions@x}]]

edited Jul 09 '14 at 19:42

answered Jul 09 '14 at 19:00

Kuba

136,707
13
279
740

1

Probably THE answer. Actually I tried Part but wasn't able to find your sequence. – eldo Jul 09 '14 at 19:06
1

This is what I thought to use as well, but please note that this does in-place modification. That's often advantageous but if you don't want it you'll have to make a copy. – Mr.Wizard Jul 09 '14 at 19:31
@Mr.Wizard I agree, now there is something different too :) – Kuba Jul 09 '14 at 19:42

score 15 · Accepted Answer · answered Jul 09 '14 at 19:21

15

Just another alternative.

x - ArrayPad[ArrayPad[x, -1], 1] // MatrixForm

answered Jul 09 '14 at 19:21

C. E.

70,533
6
140
264

2

Quite an unusual approach but I like it. – Mr.Wizard Jul 09 '14 at 19:32
3

Could also be written: x - Fold[ArrayPad, x, {-1, 1}] – Mr.Wizard Jul 09 '14 at 19:52
@Pickett Without doing any speed comparisons I would like to accept your answer because it is so clever and, like Mr. Wizard remarked, "unusual". – eldo Jul 10 '14 at 01:38
@eldo Thank you! :) – C. E. Jul 10 '14 at 09:14

score 10 · Answer 3 · answered Jul 09 '14 at 19:49

10

Although I believe that Kuba's first method is the best approach here is another:

zerofill[a_] := a (1 - BoxMatrix[#/2 - 2, #]) & @ Dimensions @ a

Now:

Array[Times, {5, 8}] // zerofill // MatrixForm

$\left( \begin{array}{cccccccc} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 2 & 0 & 0 & 0 & 0 & 0 & 0 & 16 \\ 3 & 0 & 0 & 0 & 0 & 0 & 0 & 24 \\ 4 & 0 & 0 & 0 & 0 & 0 & 0 & 32 \\ 5 & 10 & 15 & 20 & 25 & 30 & 35 & 40 \end{array} \right)$

answered Jul 09 '14 at 19:49

Mr.Wizard

271,378
34
587
1,371

1

An equivalent method: zerofill[a_?MatrixQ] := (1 - BoxMatrix[Quotient[#, 2, 1] - 1, #]) &[Dimensions[a]] a – J. M.'s missing motivation Mar 18 '18 at 09:51

ciao · Answer 4 · 2014-07-10T04:31:19.367

10

This performs quite well on large matrices, seems to outrun the others I've tested so far:

Module[{z = ConstantArray[0, Dimensions@#]},
  z[[1, All]] = #[[1, All]];
  z[[All, 1]] = #[[All, 1]];
  z[[-1, All]] = #[[-1, All]];
  z[[All, -1]] = #[[All, -1]];
  z] &

For really large arrays, it would behoove one to work in the sparse domain, where the following is even faster and certainly more memory efficient:

With[{r = First@Dimensions@#, c = Last@Dimensions@#},
  SparseArray[
   Join[Tuples[{{1}, Range@c}], Tuples[{{r}, Range@c}], 
        Tuples[{Range@r, {1}}], Tuples[{Range@r, {c}}]] -> 
    Join[#[[1]], #[[r]], #[[All, 1]], #[[All, c]]], {r, c}]] &

edited Jul 10 '14 at 04:31

answered Jul 09 '14 at 23:21

ciao

25,774
2
58
139

I never expected this to be faster than x[[2 ;; -2, 2 ;; -2]] but it is! Big +1! – Mr.Wizard Jul 09 '14 at 23:27
@Mr.Wizard: Yes, I was surprised (a bit - I expected faster, just not the degree) - but makes sense - less copy (direct or pointer) involved. I kind of like the update sparse method - even faster than the order of magnitude faster than accepted of the first (would be nice if posters specified they want 'clever' vs efficient)... Thx for +! – ciao Jul 10 '14 at 04:32
@rasher I'm sorry, I tested your code (and upvoted it), but I don't have enough experience to make reliable speed comparisons. – eldo Jul 11 '14 at 01:21

kglr · Answer 5 · 2018-01-16T00:59:14.403

MorphologicalPerimeter

x MorphologicalPerimeter[$MaxMachineNumber + x] // MatrixForm // TeXForm

$\left( \begin{array}{cccccccccc} 2 & 5 & 5 & 11 & 11 & 23 & 37 & 41 & 43 & 47 \\ 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 67 \\ 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 73 \\ 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 79 \\ 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 83 \\ 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 83 \\ 5 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 83 \\ 7 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 89 \\ 11 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 97 \\ 29 & 29 & 37 & 41 & 53 & 67 & 71 & 79 & 79 & 97 \\ \end{array} \right)$

If there are no zeros on the perimeter of the input matrix, you can use MorphologicalPerimeter[x] instead of MorphologicalPerimeter[$MaxMachineNumber + x].

# MorphologicalPerimeter[$MaxMachineNumber + #] &@RandomInteger[5, {5, 15}] // 
  MatrixForm // TeXForm

$\left(\begin{array}{ccccccccccccccc} 4 & 0 & 2 & 1 & 5 & 0 & 1 & 5 & 0 & 2 & 2 & 0 & 0 & 0 & 4 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 5 \\ 3 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 5 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\ 0 & 1 & 2 & 5 & 3 & 4 & 4 & 3 & 4 & 0 & 2 & 4 & 5 & 3 & 4 \\ \end{array}\right)$

Basheer Algohi · Answer 6 · 2014-07-09T20:22:33.747

7

n = Dimensions[x];
ReplacePart[x, {i_, j_} /;2 <= i <= n[[1]] - 1 && 2 <= j <= n[[2]] - 1 :> 0]

another way:

MapAt[0 &, x, {2 ;; -2, 2 ;; -2}]

edited Jul 09 '14 at 20:22

answered Jul 09 '14 at 20:00

Basheer Algohi

19,917
1
31
78

2

+1. Just 0 & is enough. – C. E. Jul 09 '14 at 20:07
@ Pickett, thanks for the tip :) – Basheer Algohi Jul 09 '14 at 20:18
@kuba, thanks,I have modified it for non square matrices. – Basheer Algohi Jul 09 '14 at 20:23

george2079 · Answer 7 · 2014-07-09T20:29:00.780

3

       # ArrayPad[ConstantArray[0, Dimensions@# - 2], 1, 1] &@ 
             Array[Times, {5, 8}]

or

       # SparseArray[# -> 1 & /@
           Flatten[{#, Reverse@# } &@ 
                  {_, #} & /@ {1, -1}, 1],
                    Dimensions@#] &@  Array[Times, {5, 8}]

edited Jul 09 '14 at 20:29

answered Jul 09 '14 at 20:00

george2079

38,913
1
43
110

kglr · Answer 8 · 2014-07-10T07:37:26.137

3

A variation on @rasher's post:

border = Module[{a = ConstantArray[0, Dimensions@#], i = {1, -1}}, 
                {a[[i]], a[[All, i]]} = {#[[i]], #[[All, i]]}; a] &

border@x //MatrixForm

enter image description here

and another SparseArray variation

border2 = Module[{a = ConstantArray[0, Dimensions@# - 2], d = Dimensions@#}, 
                  # SparseArray[Band[{2, 2}] -> a, d, 1]] &

edited Jul 10 '14 at 07:37

answered Jul 09 '14 at 23:58

kglr

394,356
18
477
896

Nasser · Answer 9 · 2014-07-10T07:56:08.453

3

All the good answers are given. For fun, here is one using SparseArray

 {n, m} = Dimensions[x];
 x = SparseArray[{{i_, j_} /; j == 1||j == m||i == 1||i == n} :> {x[[i, j]]}, {n, m}];
 MatrixForm[x]

Mathematica graphics

edited Jul 10 '14 at 07:56

answered Jul 10 '14 at 00:56

Nasser

143,286
11
154
359

@Kuba good point, easy to fix, will do in sec – Nasser Jul 10 '14 at 07:53

Replace interior of matrix with zeros

9 Answers9

MorphologicalPerimeter

Linked