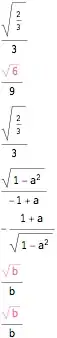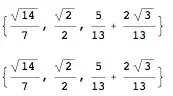25

In Mathematica 7, if I input Sqrt[2/7], Mathematica outputs $\sqrt{\frac{2}{7}}$, but I want it to output $\frac{\sqrt{14}}{7}$ instead. How do I make Mathematica output values without radicals in the denominator by default? I already tried this solution without success:

rat[p_] := If[FreeQ[Denominator[p], Power[_, Rational[_, _]]], 0, 1]
FullSimplify[Sqrt[2/7], ComplexityFunction -> rat]

I guess I need a better ComplexityFunction, and some way to have Mathematica output the rationalized form by default, instead of having to explicitly use FullSimplify every time.

edit: It would be great if the solution also worked for more complex expressions. For example: $\frac{1}{\sqrt{2}}\rightarrow\frac{\sqrt{2}}{2}$ and $\frac{1}{5-2\sqrt{3}}\rightarrow\frac{5}{13}+\frac{2\sqrt{3}}{13}$

Carl Woll
  • 130,679
  • 6
  • 243
  • 355
rmv
  • 373
  • 3
  • 7
  • I solved it for the three examples you gave. Other cases can be handled through additional replacement rules. – DavidC May 08 '12 at 01:27
  • An obvious question is why you want to rationalize the denominator? Yes, I know we were taught in school to do that, but it's not always the best thing. Even in calculus when, e.g, you calculate certain limits, the method involves rationalizing a numerator thereby unrationalizing ("irrationalizing"?) the numerator. – murray May 08 '12 at 03:50
  • @murray: I'm studying circuit analysis by solving practice problems, and the reference answers are in this form. – rmv May 09 '12 at 00:24
  • @mv: you can always apply Simplify to your answer (and, if necessary, to the reference answers) to see if they're the same -- without having to rationalize the denominators. – murray May 09 '12 at 03:30
  • I believe this has a solution (by David E Speyer) here – მამუკა ჯიბლაძე Apr 10 '18 at 09:32

7 Answers7

16

In the old days, when "making the Numerator rational" was often wanted, I came up with the following set of rules:

EvaluiereAt[pos:(_Integer|{__Integer}),f_:Identity][expr_]:=
  ReplacePart[expr,pos->Extract[expr,pos,f]];
EvaluiereAt[pos:{{__Integer}..},f_:Identity][expr_] :=
  Fold[ReplacePart[#1, #2 -> Extract[#1, #2, f]] &, expr, Reverse[Sort[pos]]];

$pinkHoldColor = ColorData["HTML"]["HotPink"];
pinkHold[x_] := Style[Tooltip[HoldForm[x], "held"], $pinkHoldColor];

Attributes[rootRational] = {Listable};
rootRational[expr_] := 
  Module[{zw, res, pos}, zw = expr /. Sqrt[a_] :> Sqrt[Together[a]];
   res = zw /. Sqrt[a_/b_] :> Sqrt[Expand[a b]]/b;
   res = res /. {a_./(b_ + d_. Sqrt[c_]) -> (a (b - d Sqrt[c]))/(b^2 -
           d^2 c), 
      a_./(b_ - d_. Sqrt[c_]) -> (a (b + d Sqrt[c]))/(b^2 - d^2 c)};
   res = res /. Sqrt[Rational[a_, b_]] :> pinkHold[Sqrt[a b]]/b;
   res = res /. (a_/Sqrt[b_]) :> a pinkHold[Sqrt[b]]/b;
   res = res /. 
     b_. Power[a_, Rational[-1, 2]] :> b pinkHold[Sqrt[a]]/a;
   pos = Position[res, _?NumberQ];
   If[Flatten[pos] =!= {}, res = EvaluiereAt[pos][res]];
   res];

Attributes[pinkUnhold] = {Listable};
pinkUnhold[expr_] := 
  ReleaseHold[expr /. Style[Tooltip[a_, __], __] -> a];

the function rootRational tries to achieve this. To show, that something is in HoldForm, I marked it with a pink color. To ReleaseHold and take away the color an tooltip there is the function pinkUnhold.

Examples:

w = Sqrt[6]/9 
% // rootRational 
% // pinkUnhold Clear[a]; 
w = Sqrt[(1 + a)/(1 - a)] // rootRational 
% // FullSimplify 
rootRational[Sqrt[b]/b] 
rootRational[1/Sqrt[b]]

Mathematica graphics

Peter Breitfeld
  • 5,182
  • 1
  • 24
  • 32
  • Could you add the definition of EvaluiereAt to your answer? After finding it here, this solution worked best so far. – rmv May 07 '12 at 22:20
  • @rmv sorry I missed to copy this definition. I've added it to my answer. – Peter Breitfeld May 07 '12 at 22:36
  • Nice feature. I would like to point out that w = Sqrt[(1 + a)^3/(1 - a)/(1 - b)] // rootRational fails in some sense. w = Sqrt[(1 + a)^3/(1 - a)/(1 - b)] // PowerExpand//rootRational gives the expected answer if a<1 and b<1 – chris Jun 09 '12 at 11:58
  • If you look into the code, you'll see, that the rules are made for squareroots. I made this for teaching purposes, not to be an ever working solution. – Peter Breitfeld Jun 09 '12 at 12:13
11

I guess the normal evaluation-process will always convert this back to $\sqrt{2/7}$ unless you hold the form explicitly. Converting your expression into the desired form can be done with Numerator and Denominator which luckily give the desired values of $\sqrt{14}$ and $7$.

Divide @@ (HoldForm /@ {Numerator[#], Denominator[#]} &[Sqrt[2/7]])

In the moment you release the HoldForm the expression gets evaluated back to $\sqrt{2/7}$.

halirutan
  • 112,764
  • 7
  • 263
  • 474
9

If you want to specifically handle expressions that are visually displayed as radicals, the most robust method I know is to manipulate the Box structure itself. Here is one way to do that using the method proposed by halirutan.

$PrePrint = 
  ToExpression[
    ToBoxes[#] /. 
     x_SqrtBox :> 
      ToBoxes[
        Divide @@ HoldForm /@ {Numerator@#, Denominator@#} & @ ToExpression @ x
      ]
  ] &;
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
4

Below are two ways to approach the problem. You could use a replacement rule with HoldForm:

rat1 = {Sqrt[Rational[n_, d_]] :>   Sqrt[n d]/HoldForm[d], 
        1/Sqrt[x_] :> Sqrt[x]/HoldForm[x], 
        1/(a_ + (b_ Sqrt[c_]) ) :> a/(a^2 - b^2 c) - (b Sqrt[c])/(a^2 - b^2 c)};

Or you could use FractionBox:

rat2 = {Sqrt[Rational[n_, d_]] :> DisplayForm@FractionBox[Sqrt[n d], d], 
        1/Sqrt[x_] :> DisplayForm@FractionBox[Sqrt[x], x], 
        1/(a_ + (b_ Sqrt[c_]) ) :> a/(a^2 - b^2 c) - (b Sqrt[c])/(a^2 - b^2 c)};

(The third rule for rat1 and rat2 is the same, and requires neither HoldForm nor FractionBox.)

Testing and showing output below:

{Sqrt[2/7], 1/Sqrt[2], 1/(5 - 2 Sqrt[3])} /. rat1
{Sqrt[2/7], 1/Sqrt[2], 1/(5 - 2 Sqrt[3])} /. rat2

results

DavidC
  • 16,724
  • 1
  • 42
  • 94
3

Based on MinimalPolynomial for more complicated case:

rootRational[fraction_] := 
 Module[{numer = Numerator[fraction], denon = Denominator[fraction], 
   poly, x}, poly = MinimalPolynomial[denon, x]; 
  FullSimplify[Times[numer, Rest[poly]/-x/First[poly] /. x -> denon]]]

Usage

rootRational[1/(Sqrt[2] + Sqrt[3] + Sqrt[5])]


rootRational[7/(
 6 - 6 Sqrt[2] + 5 Sqrt[3] + 3 Sqrt[5] - 2 Sqrt[6] - 3 Sqrt[10] + 
  2 Sqrt[15] - Sqrt[30])]

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
yode
  • 26,686
  • 4
  • 62
  • 167
3

For displaying algebraics where the denominator is a simple radical, you can override the formatting of Times/Power:

Clear[MakeBoxes];
MakeBoxes[a_. Power[b_, r_Rational?Negative], fmt_] := With[
    {p = Mod[r, 1], pow = Quotient[r, 1]},
    MakeBoxes[Times[a, b^pow, Defer[Power[b,p]]], fmt]
]

Examples:

{1/Sqrt[2], 5/Power[3, (3)^-1], 1/(2+3/Sqrt[5])} //TeXForm

$\left\{\frac{\sqrt{2}}{2},\frac{5\ 3^{2/3}}{3},\frac{1}{2+\frac{3 \sqrt{5}}{5}}\right\}$

I didn't bother extending this to your more complicated examples, because having:

1/(5 - 2 Sqrt[3])

automatically display as:

5/13 + (2 Sqrt[3])/13

would be very confusing (what should First return?) Instead, I think it makes much more sense to have a function that converts the expression into a rationalized form, e.g., see question 9868.

Carl Woll
  • 130,679
  • 6
  • 243
  • 355
2

I found this function by Andrzej Kozlowski in the MathGroup Archive:

f1[expr_] :=
  FullSimplify[expr, ComplexityFunction ->
    (
      Count[#, _?
        (MatchQ[Denominator[#], Power[_, _Rational] _. + _.] &),
        {0, Infinity}
      ] + If[FreeQ[#, Root], 0, 1] &
    )
  ]

A combination of this, Expand, and Peter Breitfeld's solution seems to work best. E.g.:

test $=\{\frac{2}{3\sqrt{5}},\frac{1}{2-\frac{3}{\sqrt5{}}},\frac{1}{2-\frac{3}{5+\sqrt{7}}}\}$

test // f1 // Expand // rootRational

$\{\frac{2\sqrt{5}}{15},\frac{10}{11}+\frac{3\sqrt{5}}{11},1-\frac{\sqrt{7}}{7}\}$

rmv
  • 373
  • 3
  • 7