In a strict meaning the answer is no.
A mathematical concept of a set is so basic and general, that one even cannot imagine most of sets and the more it concerns the possibility of their computer representations. For some hints of surprising properties of infinite sets see e.g. Continuum Hypothesis or Gödel's theorem. If you relate your question to finite sets then the answer is certainly yes.
There is only some kind of resemblance between finite sets and Mathematica lists.
Of course we can represent sets as lists (see e.g. Lists as Sets), but some adequate functions treats them not quite like pure sets (i.e. completely orderless), but rather like lists (i.e. with ordering) :
A = {1, 2, 6, 7, 3};
B = {1, 3, 2, 7, 6};
{A === B, Sort[A] === Sort[B]}
{False, True}
I suggest to take a closer look at these functionalities :
Union, Intersection, Complement, Subsets etc. being Mathematica counterparts of the basic set theory operations. Intersection gives a sorted list of the common elements, while Union[A] gives a sorted version of a "set" A, moreover it can be used with an option SameTest. These functions work with finite sets, so in principle they cannot be equivalent to mathematical concepts of the set theory.
We can use this to test wether given two "sets" are identical :
Intersection[A, B] === Sort[A] === Sort[B]
True
Representation of infinte sets is a bit more difficult and of course we cannot represent infinite sets as lists, e.g. solving an equation with an infinite number of solutions we get an output in the boolean form :
Reduce[ Sin[x] == 1/2, x]
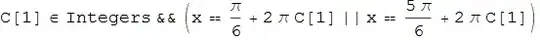
while Solve returning solutions as a list of rules :
Solve[ Sin[x] == 1/2, x]
yields only one solution with a message saying that some solutions may not be found.
Therefore the above difference is quite analogical to symbolic representation of $\pi$ and its decimal expansion - there is an infinite number of digits to represent but we can process only finite number of them.
So to define symbolically a set of functions you have to decide what kind of set
it is. A series of functions can be defined (or enumerated) by natural numbers, but elements of uncountable sets cannot be ennumerated, and you should know that spaces of functions (Hilbert, Banach, etc. ) are uncountable. See e.g. Cantor's theorem
A true challenge would be some kind of representation of unmeasurable sets. See e.g. Banach-Tarski theorem and its constructive toy counterpart by Stan Wagon.
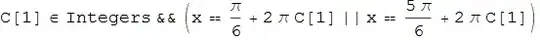
OrderedQfunction. Two distinct Mathematica expressions will always have a well defined, though possibly surprising ordering based on this built-in comparison function. Please see here. – Szabolcs May 08 '12 at 12:36Realsand it concerns also numbers or solutions of equations. You can of course make some mapping to enumerate functions, but only countable sets of functions (e.g. series of functions), uncountable ones are basically impossible to enumarate. See my answer for more details and some useful links. – Artes May 08 '12 at 23:18