Point Belonging to a Disk in a Cartesian Coordinate System

Question

The image below represents a human subject fixations while observing this abstract pattern for 3 seconds.

I would like to know how much time they spent looking at the actual disk. That is a red point within a Black Disk.

enter image description here

Each fixations (each sublist of "fixations" below is coded as such : {{x,y}, Duration in ms}.

 fixations=
 {{{20.3899, 14.8931}, 238}, {{27.0063, 18.8899},428}, 
  {{25.8113, 24.8679}, 377}, {{24.2579, 22.022},106}, 
  {{25.3208, 24.022}, 130}, {{21.739, 12.1792},175}, 
  {{29.2673, 8.88994}, 295}, {{30.3868, 17.6572},160}, 
  {{31.217, 22.6761}, 145}, {{22.9686, 20.6918},155}, 
  {{19.6321, 20.2704}, 145}}

Each Disk is coded as {x, y, radius}.

 Disks=
 {{22.8176, 19.9696, 0.974938}, {29.5314, 10.7197, 0.974938}, 
  {17.5112,19.7207, 0.974938}, {30.8997, 23.2454, 0.974938},
  {28.0588,6.09759, 0.974938}, {30.8524, 17.0661, 1.53205}, 
  {21.0393, 10.7137,1.53205}, {25.451, 25.1336, 1.53205}}

How could I :

Count the number of fixations that are within a disk.
Then how much actual time they spent there.

The only solution I thought about was to compute the EuclideanDistance of each fixation to each disk but I feel there is a smarter faster way to do this.

Thank you for your attention.

Are overlapping disks possible? That would influence the algorithms (multiple hit counts). — Yves Klett, May 08 '12 at 15:41
See http://mathematica.stackexchange.com/questions/2711/clustering-of-space-time-data for some techniques closely related to this question. — whuber, May 08 '12 at 17:56

Yves Klett · Accepted Answer · 2012-05-08T14:08:16.007

Edit: Version 1 using Nearest

I think Nearest can be put to good use here anyway. This one uses the idea (inspired by @DanielLichtblau) that you can carry useful information in a NearestFunction that is not relevant for the actual distance by scaling those values with a small factor, finding the nearest points/vectors and the re-scaling the stowaways. While this is not exact, it can be very useful if you want to use "mixed" vectors and still get the performance gained by repeated use of a NearestFunction (here together with timing information).

Slight reformatting (scaling time with small factor):

fixations2 = Flatten[#]*{1, 1, 2^-20} & /@ fixations;

adding a 0 for compatibility...

Disks2 = Insert[#, 0, 3] & /@ Disks;

here we go (NearestFunction nf is called with additional arguments {n, radius}):

nf = Nearest[fixations2];

hits = Map[#*{1, 1, 2^20} &, 
   nf[#[[1 ;; 3]], {Infinity, #[[-1]]}] & /@ Disks2, {2}][[All, All, 
   3 ]]

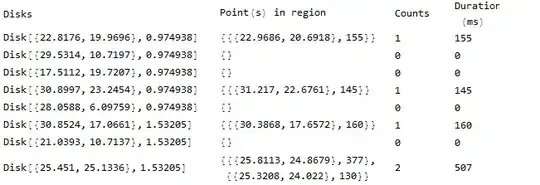
{{155}, {}, {}, {145}, {}, {160}, {}, {377, 130}}

Total /@ hits

{155, 0, 0, 145, 0, 160, 0, 507}

This should scale pretty well with larger samples.

Version 2 (straightforward)

Another, very simple version with a bit of pattern mumbo-jumbo for versatile use with different input types (will become slow for large sample numbers):

fixations = {{{20.3899, 14.8931}, 238}, {{27.0063, 18.8899}, 
    428}, {{25.8113, 24.8679}, 377}, {{24.2579, 22.022}, 
    106}, {{25.3208, 24.022}, 130}, {{21.739, 12.1792}, 
    175}, {{29.2673, 8.88994}, 295}, {{30.3868, 17.6572}, 
    160}, {{31.217, 22.6761}, 145}, {{22.9686, 20.6918}, 
    155}, {{19.6321, 20.2704}, 145}};

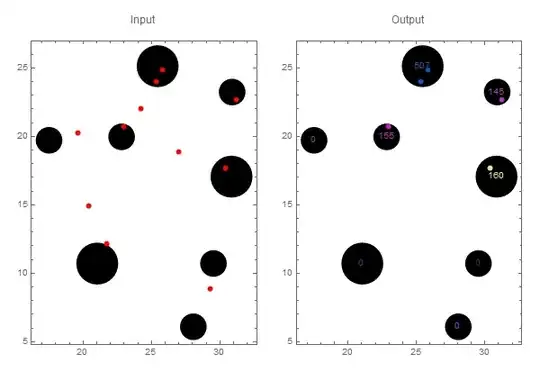
Disks = {{22.8176, 19.9696, 0.974938}, {29.5314, 10.7197, 
    0.974938}, {17.5112, 19.7207, 0.974938}, {30.8997, 23.2454, 
    0.974938}, {28.0588, 6.09759, 0.974938}, {30.8524, 17.0661, 
    1.53205}, {21.0393, 10.7137, 1.53205}, {25.451, 25.1336, 1.53205}};

timeindisk[{{x_?NumericQ, y_?NumericQ}, time_}, {u_?NumericQ, 
   v_?NumericQ, r_?NumericQ}] := 
 If[Norm[{x, y} - {u, v}] <= r, time, 0]

timeindisk[#, Disks[[1]]] & /@ fixations

{0, 0, 0, 0, 0, 0, 0, 0, 0, 155, 0}

Threaded over fixes:

timeindisk[fixes_List, {u_?NumericQ, v_?NumericQ, r_?NumericQ}] := 
 timeindisk[#, {u, v, r}] & /@ fixes

timeindisk[fixations, Disks[[1]]]

{0, 0, 0, 0, 0, 0, 0, 0, 0, 155, 0}

Threaded over fixes and disks:

timeindisk[fixes_List, disks_List] := timeindisk[fixes, #] & /@ disks

times = timeindisk[fixations, Disks]

{{0, 0, 0, 0, 0, 0, 0, 0, 0, 155, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 145, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 160, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 0, 377, 0, 130, 0, 0, 0, 0, 0, 0}}

(*    Time within disks: Total*)
Total /@ times

{155, 0, 0, 145, 0, 160, 0, 507}

Rojo · Answer 2 · 2012-05-08T12:56:00.657

This is neither ingenious nor pretty, but I guess it should be fast (not sure if faster or how much faster than Nearest based approaches, haven't tested), if you need to compute a lot and the compile time is not important. It stops checking when it has already found a fixation in a disk (so, assumed no-overlap)

isInDiskCmp = 
  Compile[{{pt, _Real, 1}, {disks, _Real, 2}}, 
   Module[{is = 0.}, 
    Do[If[Total[(i[[1 ;; 2]] - pt)^2] < i[[3]]^2, is = 1.; 
      Break[]], {i, disks}]; is], CompilationTarget -> "C", 
   RuntimeAttributes -> Listable, Parallelization -> True];

To see which fixations lied in a disk

fixationsInDisk=isInDiskCmp[fixations[[All, 1]], disks] == 1.//Thread

To count the total time spent in disks

Total[Pick[fixations[[All, 2]], fixationsInDisk]]

score 4 · Answer 3 · edited Apr 13 '17 at 12:56

pointsInDisk = Function[{dsk}, 
Pick[fixations, UnitStep[Norm[#[[1]] - dsk[[;; 2]]] - dsk[[3]]] & /@ fixations, 0]];

Usage:

pointsInDisk/@Disks

gives

{{{{22.9686, 20.6918}, 155}}, {}, {}, {{{31.217, 22.6761},145}}, {}, 
  {{{30.3868, 17.6572}, 160}}, {}, {{{25.8113, 24.8679}, 377}, {{25.3208, 24.022}, 130}}}

Counts and durations in disks:

{Length@#, If[# == {}, 0, Total[Last /@ #]]} & /@ (pointsInDisk /@ Disks)
(* output: *)
{{1, 155}, {0, 0}, {0, 0}, {1, 145}, {0, 0}, {1, 160}, {0, 0}, {2, 507}}

Note: For large lists replacing the argument of UnitStep inside Pick with

Sqrt[Inner[Times, #[[1]] - dsk[[;; 2]], #[[1]] - dsk[[;; 2]], Plus]] - dsk[[3]]

or

Sqrt[Total[Function[{y}, y^2] /@ (#[[1]] - dsk[[;; 2]])]] - dsk[[3]]

may improve timings (see, for example, this).

Syed · Answer 4 · 2023-09-08T09:11:43.170

Using Outer and RegionMember:

Clear["Global`*"];
fixations = {{{20.3899, 14.8931}, 238}, {{27.0063, 18.8899}, 
   428}, {{25.8113, 24.8679}, 377}, {{24.2579, 22.022}, 
   106}, {{25.3208, 24.022}, 130}, {{21.739, 12.1792}, 
   175}, {{29.2673, 8.88994}, 295}, {{30.3868, 17.6572}, 
   160}, {{31.217, 22.6761}, 145}, {{22.9686, 20.6918}, 
   155}, {{19.6321, 20.2704}, 145}};
Disks = {{22.8176, 19.9696, 0.974938}, {29.5314, 10.7197, 
   0.974938}, {17.5112, 19.7207, 0.974938}, {30.8997, 23.2454, 
   0.974938}, {28.0588, 6.09759, 0.974938}, {30.8524, 17.0661, 
   1.53205}, {21.0393, 10.7137, 1.53205}, {25.451, 25.1336, 1.53205}};
disks = Disk[{#1, #2}, #3] & @@@ Disks (* to make these proper Region  entities*)

(* to find out which fixations are inside which disks *)

inside = Outer[RegionMember[#1, #2] &, disks, fixations[[All, 1]] , 1]
picks = Pick[fixations, #] & /@ inside
totals = picks[[All, All, -1]] // Map[Total]
counts = picks // Map[Length]
(res = Transpose[{disks, picks, counts, totals}]) //
 Grid[Prepend[#, {"Disks", "Point(s) in region", "Counts", 
     "Duration\n (ms)"}]
   , Alignment -> {Left, Center}
   , ItemSize -> {{20, 16, 5, 5}, 1.3}
   ] &

Visualization

SeedRandom[1];
GraphicsRow[{
  Graphics[{
    disks
    , Red, AbsolutePointSize[6]
    , Point@First@# & /@ fixations
    }
   , Frame -> True
   , PlotLabel -> "Input"
   ]
  ,
  Graphics[{
    MapThread[{Black, #1, RandomColor[]
       , AbsolutePointSize[6], Point@#2[[All, 1]]
       , Text[#4, #1[[1]]]} &
     , Transpose@res
     ] (* end of MapThread *)
    }
   , Frame -> True
   , PlotLabel -> "Output"
   ]
  }]

Point Belonging to a Disk in a Cartesian Coordinate System

4 Answers4