Minimize loop optimization

Question

I'm new in Mathematica 10.

So far, I have a two variable-function and I've use Minimize to find the optimal solution.

Nevertheless, I'd like to make a sensibility analysis and study how this optimal solution behaves, doing a "For" cycle changing some coefficient of this function and keeping all the optimal solution in a table or matrix.

Is that possible to do? I've tried using a For cycle but I don't know how to save the optimal value in an auxiliary variable.

For instance :

Table[NMinimize[{a x + b y, 0.2 x + 0.1 y >= 14, 0.25 x + 0.6 y >= 30, 
    0.1 x + 0.15 y >= 10, x >= 0, y >= 0}, {x, y}][[2]], {a, 0, 3, 1}, {b, 0, 3, 1}]

Does anyone one how to save all of the X and Y Values in only 2 columns? I'd like to associate those columns to de corresponding value of a and b

Answer 1

I'm not sure exactly what you want, but in an effort to demonstrate some possibilities:

Join @@ Table[{{a, b}, 
    NMinimize[{a x + b y, 0.2 x + 0.1 y >= 14, 0.25 x + 0.6 y >= 30, 0.1 x + 0.15 y >= 10,
        x >= 0, y >= 0}, {x, y}][[2]]}, {a, 0, 3, 1}, {b, 0, 3, 1}] // Column

Or:

Join @@ Table[{{HoldForm[a] -> a, HoldForm[b] -> b}, 
    NMinimize[{a x + b y, 0.2 x + 0.1 y >= 14, 0.25 x + 0.6 y >= 30, 0.1 x + 0.15 y >= 10,
        x >= 0, y >= 0}, {x, y}][[2]]}, {a, 0, 3, 1}, {b, 0, 3, 1}] // MatrixForm

---

Based on your comment perhaps:

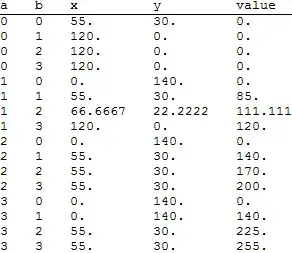
expr =
  {a x + b y, 0.2 x + 0.1 y >= 14, 0.25 x + 0.6 y >= 30, 0.1 x + 0.15 y >= 10, x >= 0, y >= 0};

tab =
  Table[
    {a, b, x, y, #} /. #2 & @@ NMinimize[expr, {x, y}],
    {a, 0, 3}, {b, 0, 3}
  ] ~Flatten~ 1;

TableForm[tab, TableHeadings -> {None, {"a", "b", "x", "y", "value"}}]

If wish to use specific values rather than a range you merely need this syntax for Table:

For example:

aVals = RandomInteger[{0, 20}, 7]

{3, 9, 4, 5, 18, 13, 3}

expr =
  {a x + b y, 0.2 x + 0.1 y >= 14, 0.25 x + 0.6 y >= 30, 0.1 x + 0.15 y >= 10, x >= 0, y >= 0};

tab =
  Table[
    {a, b, x, y, #} /. #2 & @@ NMinimize[expr, {x, y}],
    {a, aVals}, {b, 0, 3}
  ] ~Flatten~ 1;

TableForm[tab, TableHeadings -> {None, {"a", "b", "x", "y", "value"}}]

---

Explanation

brama requested an explanation of this code:

I have trouble understanding the role of #2 and ~Flatten~ 1. Also, How does it transfer the optimal x and y values from the NMinimize to the table?

The documentation for NMinimize states:

The first part is the minimum value found, and the second part is a list of replacement rules.

I used the combination of Function, Slot, and Apply to handle these two parts. An independent example:

{a, b, x, y, #} /. #2 & @@ {"part1", "part2"} // Quiet

{a, b, x, y, "part1"} /. "part2"

(I used Quiet to suppress the message informing us that "part2" is not a list of replacement rules.)

With actual output from NMimimize: {0., {x -> 55., y -> 30.}} this becomes:

{a, b, x, y, 0.} /. {x -> 55., y -> 30.}

Then after the ReplaceAll replacements and evaluation of a and b within Table:

{0, 0, 55., 30., 0.}

See this answer for other ways to work with the output of NMinimze.

The final piece of the code is ~Flatten~ 1. First: a ~op~ b is infix notation for op[a, b]. Flatten is used to combine expressions with the same head (by default List) and different levels. Here it is used to combine the lists of solutions for each a value into a single list of solutions. An independent example:

x1 = Array[Plus, {3, 4, 5}]

{{{3, 4, 5, 6, 7}, {4, 5, 6, 7, 8}, {5, 6, 7, 8, 9}, {6, 7, 8, 9, 10}},
 {{4, 5, 6, 7, 8}, {5, 6, 7, 8, 9}, {6, 7, 8, 9, 10}, {7, 8, 9, 10, 11}},
 {{5, 6, 7, 8, 9}, {6, 7, 8, 9, 10}, {7, 8, 9, 10, 11}, {8, 9, 10, 11, 12}}}

x1 ~Flatten~ 1

{{3, 4, 5, 6, 7},
 {4, 5, 6, 7, 8},
 {5, 6, 7, 8, 9},
 {6, 7, 8, 9, 10},
 {4, 5, 6, 7, 8},
 {5,6, 7, 8, 9},
 {6, 7, 8, 9, 10},
 {7, 8, 9, 10, 11},
 {5, 6, 7, 8, 9},
 {6, 7, 8, 9, 10},
 {7, 8, 9, 10, 11},
 {8, 9, 10, 11, 12}}

Answer 2

How about this?

Grid[Prepend[
  Flatten[Table[{a, b, 
      Reverse@NMinimize[{a x + b y, 0.2 x + 0.1 y >= 14, 
         0.25 x + 0.6 y >= 30, 0.1 x + 0.15 y >= 10, x >= 0, 
         y >= 0}, {x, y}]}, {a, 0, 3, 1}, {b, 0, 3, 1}] /. {ap_, 
      bp_, {{x -> xp_, y -> yp_}, axbyp_}} :> {ap, bp, xp, yp, axbyp},
    1], {"a", "b", "x", "y", "CT"}], Frame -> All]