9

Is it possible to compute trapezoidal rule numerical integration? I know that Mathematica has Interpolation, and that a list of points can be interpolated and then integrated simply using Integrate. However, my functions are highly oscillatory (they are based on simulation data), and I am not convinced that the interpolation is perfect, even when I set WorkingPrecision to a very high value. Also, I know that ListIntegrate is deprecated, and even if I use it, I am not certain if it is using the trapezoidal rule, which I would like to use.

Do you know if any resources where I can find Mathematica or pseudocode for trapezoidal integration of lists of points? Or do you have any suggestions about how I can use Mathematica efficiently to program such an algorithm myself?

Thanks!

AsukaMinato
  • 9,758
  • 1
  • 14
  • 40
Andrew
  • 10,569
  • 5
  • 51
  • 104
  • 1
    Why not start at the obvious place: http://en.wikipedia.org/wiki/Trapezoidal_rule – rm -rf May 16 '12 at 15:51
  • 2
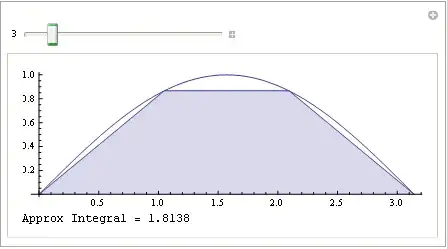
    Actually NIntegrate[] indeed is able to perform the trapezoidal rule (see docs for details). I suspect that it won't be the best method for your problem; why not elaborate a bit more on these oscillatory functions you speak of? – J. M.'s missing motivation May 16 '12 at 15:53
  • 2
    Might check Documentation Center > Integrationtutorial/NIntegrateIntegrationStrategies#144042466 and tutorial/NIntegrateIntegrationRules#32844337 for some ideas on option setting for NIntegrate of finite region oscillatory functions. – Daniel Lichtblau May 16 '12 at 17:04

3 Answers3

20
t = Table[{x, Sin[x]}, {x, 0, Pi, .01}];
1/2 Total[((#[[2, 1]] - #[[1, 1]]) (#[[2, 2]] + #[[1, 2]])) & /@  Partition[t, 2, 1]]
(*
-> 1.99998
*)

Perhaps better

1/2 Total[Differences[t[[All, 1]]] ListCorrelate[{1, 1}, t[[All, 2]]]]

They are just

$$\int_a^b f(x)\,dx\approx\frac12\sum_{k=1}^N (x_{k+1}-x_k)(f(x_{k+1})+f(x_k))$$

Edit

Just for fun, using JM's shorter expression:

Manipulate[
   Column[{
     Show[Plot[Sin[x], {x, 0, Pi}], ListLinePlot[#, Filling -> Axis],
         AspectRatio -> Automatic, ImageSize -> 400], 
     Row[{"Approx Integral = ",N@Differences[#1].MovingAverage[#2, 2]& @@ Transpose[#]}]}]&@
     Table[{x, Sin[x]}, {x, 0, Pi, Pi/a}],
 {{a, 2, Dynamic[a]}, 2, 10, 1}]

enter image description here

Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453
3

The following is quite fast on packed arrays: 

(Rest@Last@# + Most@Last@#).(Rest@First@# - Most@First@#)/2 &@
 Transpose[t]

Small example:

t = Developer`ToPackedArray@
   Table[{x, Sin[x]}, {x, Subdivide[0., Pi, 100]}];

Differences[#1].MovingAverage[#2, 2] & @@ Transpose[t] //
 RepeatedTiming
1/2 Total[Differences[t[[All, 1]]] ListCorrelate[{1, 1}, t[[All, 2]]]] //
 RepeatedTiming
(Rest@Last@# + Most@Last@#).(Rest@First@# - Most@First@#)/2 &@ Transpose[t] //
 RepeatedTiming
(*
  {0.000036, 1.99984}
  {0.000014, 1.99984}
  {8.5*10^-6, 1.99984}
*)

Larger example (autocompiled by Table, which produces a packed array):

t = Table[{x, Sin[x]}, {x, Subdivide[0., Pi, 10000]}];

Differences[#1].MovingAverage[#2, 2] & @@ Transpose[t] //
 RepeatedTiming
1/2 Total[Differences[t[[All, 1]]] ListCorrelate[{1, 1}, t[[All, 2]]]] //
 RepeatedTiming
(Rest@Last@# + Most@Last@#).(Rest@First@# - Most@First@#)/2 &@ Transpose[t] //
 RepeatedTiming
(*
  {0.0004, 2.}
  {0.00050, 2.}
  {0.000093, 2.}
*)
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Super. Your Method "Rest@Last@ ..." is very fast. Would you kindly show use how to use this for an vector of functions like{Sin[x],Cos[x],Tan[x]} . – Gummala Navneeth Dec 28 '20 at 15:38
  • 1
    @GummalaNavneeth Perhaps xx = Subdivide[0., Pi/4., 100]; vv = {Sin[x], Cos[x], Tan[x]} /. x -> xx // Developer`ToPackedArray; (vv[[All, 2 ;;]] + vv[[All, ;; -2]]) . (Rest@xx - Most@xx)/2, if you get to generate the data. Advantage of converting to a packed array diminishes as the length of xx approaches 10^6, at which point it becomes a disadvantage. – Michael E2 Dec 28 '20 at 16:09
1

The Wolfram Demonstrations Project has this demo. It might provide an idea or two to help.

Jagra
  • 14,343
  • 1
  • 39
  • 81