How to group each element with each consecutive elements in one head

Question

Suppose I have the following list:

list = {a, b, c, d}

I want to generate this result:

{{f[a, a], f[a, b], f[a, c], f[a, d]}, {f[b, b], f[b, c],
  f[b, d]}, {f[c, c], f[c, d]}, {f[d, d]}}

What could be the shortest way?

The list elements can be anything and not necessarily sorted.

Answer 1

How about a simple table?

Table[f @@ list[[{i, j}]], {i, 4}, {j, i, 4}]

If you want to use this for a general list, you should use Length[list] in the table iterators or maybe:

With[{n = Length[list]},
 Table[f @@ list[[{i, j}]], {i, n}, {j, i, n}]
]

Answer 2

Solutions

---

Pick[
 Outer[f, list, list],
 UpperTriangularize@ConstantArray[True, {#, #} &@Length@list]
 ]

Using the new Composition shorthand:

Thread@*f @@@ MapIndexed[{#, list[[First@#2 ;;]]} &, list]

Timings

---

Testing with

list = Range[1000];

the first method takes 0.363 seconds to complete and the second takes 0.120 to complete. As a comparison, halirutan's Table method took 1.183 to complete. RunnyKine's is the fastest I have tested of the others, taking just 0.336 to complete. All times were measured with AbsoluteTiming.

Answer 3

This is not the shortest, but faster than all except Pickett's (almost just as fast)

f4 = Thread@f[#[[1]], #] & /@ Partition[#, Length@#, 1, {1, 1}, {}] &

OR

 dP = Developer`PartitionMap;

Then:

f5 = dP[Thread@f[#[[1]], #] &, #, Length@#, 1, {1, 1}, {}] &

Timings:

Needs["GeneralUtilities`"]

f1 = With[{n = Length[#]}, Table[f @@ #[[{i, j}]], {i, n}, {j, i, n}]] &; 

f2 = MapIndexed[#[[#2[[1]] ;;]] &, Outer[f, #, #]] &;

f3[x_] := Thread@*f @@@ MapIndexed[{#, x[[First@#2 ;;]]} &, x];

BenchmarkPlot[{f1, f2, f3, f4, f5}, RandomInteger[999, #] &, 2^Range[12

Answer 4

I don't believe anyone has posted exactly this formulation:

MapIndexed[#[[#2[[1]] ;;]] &, Outer[f, #, #]] &

Not terribly efficient but the question asked for shortest, not fastest.

---

Argument

Although not optimal my method is both more efficient and shorter than the presently Accepted one.
The question clearly asked for the shortest way. You should not alter your standard after the fact.

Update: also including Pickett's code

Please consider:

f1 = With[{n = Length[#]}, Table[f @@ #[[{i, j}]], {i, n}, {j, i, n}]] &; 

f2 = MapIndexed[#[[#2[[1]] ;;]] &, Outer[f, #, #]] &;

f3[x_] := Thread@*f @@@ MapIndexed[{#, x[[First@#2 ;;]]} &, x];

Needs["GeneralUtilities`"]

BenchmarkPlot[{f1, f2, f3}, RandomInteger[999, #] &, 2^Range[12]]

Answer 5

A few obfuscations via Listable:

Block[{f, op},
 SetAttributes[f, Listable];
 op[x_] := {f[x, x]};
 op[x_, y__] := Sequence[f[x, {x, y}], op[y]];
 {op @@ list}
 ]


Block[{f},
 SetAttributes[f, Listable];
 f @@@ Table[{list[[i]], list[[i ;;]]}, {i, 4}]
 ]


Module[{op1, op2},
 op1 = Function[{x, l}, f[x, l], Listable];
 op2 = {op1[#, {##}], Sequence @@ If[{##2} =!= {}, op2[##2], {}]} &;
 op2 @@ list
 ]

Update

The second method above is actually pretty good. The others aren't bad, but they are limited by $RecursionLimit. This one is slightly faster:

f4 = Block[{f},
    SetAttributes[f, Listable];
    f[First[#], #] & /@ NestList[Rest, #, Length[#] - 1]
    ] &;

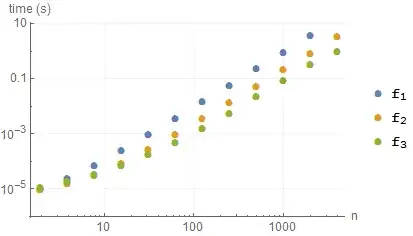
Timings

Adding to Mr.Wizard's comparison:

f1 = With[{n = Length[#]}, 
    Table[f @@ #[[{i, j}]], {i, n}, {j, i, n}]] &;

f2 = MapIndexed[#[[#2[[1]] ;;]] &, Outer[f, #, #]] &;

f3[x_] := Thread@*f @@@ MapIndexed[{#, x[[First@#2 ;;]]} &, x];

f4 = Block[{f},
    SetAttributes[f, Listable];
    f[First[#], #] & /@ NestList[Rest, #, Length[#] - 1]
    ] &;

Needs["GeneralUtilities`"]

BenchmarkPlot[{f1, f2, f3, f4}, RandomInteger[999, #] &, 2^Range[12]]

Answer 6

A few more just for fun:

ReplaceList[list, {___, a__} :> Thread @ f[#& @ a, {a}]]

Thread @* f ~MapThread~ {list, NestList[Rest, list, 3]}

Pick[Outer[f, list, list], # <= #2 & ~Array~ {4, 4}]

Answer 7

There is probably something neater but the following works:

l = {a, b, c, d};
s = SplitBy[Tuples[l, {2}], First];
list = Take[s[[#]], #2] & @@@ Thread@{Range@Length@l, Range[-Length@l, -1]}
Map[f[Sequence @@ #] &, list, {-2}]

{{f[a, a], f[a, b], f[a, c], f[a, d]}, {f[b, b], f[b, c], f[b, d]}, 
 {f[c, c], f[c, d]}, {f[d, d]}}

Answer 8

Here is a straightforward implementation...

Table[Table[f[list[[i]], list[[j]]], {j, i, Length@list}], {i, Length@list}]

Here is my flattened table: If list is a sorted list of unique elements

list = {a, b, c, d}
g[a_, b_] := f @@ Sort@{a, b};
Union@Flatten@Outer[g, list, list]

Answer 9

Thread[f[First@#, #]] & /@ 
 NestList[Drop[#, 1] &, list, Length[list] - 1]

The above is a refinement of less efficient 1st attempt:

First@Outer[f, #, #] & /@ 
 NestList[Drop[#, 1] &, list, Length[list] - 1]

Answer 10

Outer[f, list, list] /. 
 f[x_, y_] /; 
   First@First@Position[list, x] >  First@First@Position[list, y] :> 
  Sequence[] 

What's annoying here is projecting #[[1,1]]&. How to make {{1}} <= {{2}} evaluate True?

Answer 11

Building up an Association

len=Length@list;
asso=<||>;
(asso[#]=list[[-#]])&/@Range@len;

and then

Array[Function[x,Array[f[x,#]&,x,{x,1}]],len,{len,1}]/.asso

Answer 12

Throwing my hat to the ring

Clear[splitList]
splitList[f_, list_List] := 
 SplitBy[DeleteDuplicates[Sort /@ Tuples[Sort[Hold[f] @@ list], 2]], First] // ReleaseHold

splitList[f, {a, b, c, d}]
(* {{f[a, a], f[a, b], f[a, c], f[a, d]}, {f[b, b], f[b, c], 
  f[b, d]}, {f[c, c], f[c, d]}, {f[d, d]}} *)

splitList[Plus, {a, b, c, d}]
(* {{2 a, a + b, a + c, a + d}, {2 b, b + c, b + d}, {2 c, c + d}, {2 d}} *)

Answer 13

f1 = SplitBy[Tuples[f @@ #, 2] /. ( f[x__] /; Not[OrderedQ[{x}]] :> (## &[])), First]& 

f1 @ list // Grid // TeXForm

$\begin{array}{cccc} f(a,a) & f(a,b) & f(a,c) & f(a,d) \\ f(b,b) & f(b,c) & f(b,d) & \text{} \\ f(c,c) & f(c,d) & \text{} & \text{} \\ f(d,d) & \text{} & \text{} & \text{} \\ \end{array}$

Also

f2[l_] := Module[{i = 1, j}, Thread[j = i++; f[l[[j]], l[[j ;;]]]] & /@ l]

f2 @ list == f1 @ list

True