Forming an upper triangular matrix from the elements of a list

Question

I asked this question before, but i was closed because it the question was not comprehensible enough. So i reworded it, hope that's ok.

I have a list with 6 elements.

{a1, a2, a3, a4, a5, a6}

Now, I want to generate a upper triangle matrix with the elements above as matrix elements, so that the matrix reads

{{a1, a4, a6}, {0, a2, a5}, {0, 0, a3}}

That is, the triangle upper matrix matrix shall be filled up with the elements of the list. It is not important where each element is placed.

I want to do this also with larger matrices, so for example a list with 36 elements shall form a 8 x 8 upper triangle matrix.

Any ideas?

Mr.Wizard · Answer 1 · 2014-08-03T00:02:29.267

12

For the filling pattern you showed:

x = {a1, a2, a3, a4, a5, a6};

n = 3;

x ~Internal`PartitionRagged~ Range[n, 1, -1] ~Flatten~ {2} // PadLeft

{{a1, a4, a6}, {0, a2, a5}, {0, 0, a3}}

To find n given a complete input list x you can use:

n = Sqrt[1 + 8 Length@x]/2 - 1/2

edited Aug 03 '14 at 00:02

answered Aug 02 '14 at 14:52

Mr.Wizard

271,378
34
587
1,371

I get the same result without the Flatten which would make your +1 answer even shorter. – eldo Aug 02 '14 at 15:00
@eldo Thanks for vote. However Flatten is needed for the filling order shown in the question. I'll leave the "any order" filling to others, unless I think of something particularly clean. – Mr.Wizard Aug 02 '14 at 15:05
@Mr.Wizard you many need to generalize n. +1 for the Partition trick. – Basheer Algohi Aug 02 '14 at 15:09
@Algohi Updated. – Mr.Wizard Aug 03 '14 at 00:02

Öskå · Answer 2 · 2014-08-02T14:18:21.103

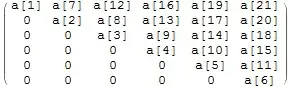
Since "It is not important where each element is placed":

a = {a1, a2, a3, a4, a5, a6}
mat = SparseArray[
        Rule[#, #2] & @@@ Thread@{Flatten[Table[{i, j}, {i, 3}, {j, i, 3}], 1], a}];
mat // MatrixForm

$\left( \begin{array}{ccc} \text{a1} & \text{a2} & \text{a3} \\ 0 & \text{a4} & \text{a5} \\ 0 & 0 & \text{a6} \\ \end{array} \right)$

If you have a list of 36 elements that you want to turn into a 8x8 upper triangle matrix:

l = Range@36;
mat = SparseArray[
   Rule[#, #2] & @@@ Thread@{Flatten[Table[{i, j}, {i, 8}, {j, i, 8}], 1], l}];
mat // MatrixForm

$\left( \begin{array}{cccccccc} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 0 & 9 & 10 & 11 & 12 & 13 & 14 & 15 \\ 0 & 0 & 16 & 17 & 18 & 19 & 20 & 21 \\ 0 & 0 & 0 & 22 & 23 & 24 & 25 & 26 \\ 0 & 0 & 0 & 0 & 27 & 28 & 29 & 30 \\ 0 & 0 & 0 & 0 & 0 & 31 & 32 & 33 \\ 0 & 0 & 0 & 0 & 0 & 0 & 34 & 35 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 36 \\ \end{array} \right)$

Here is an attempt to make it more robust:

mat[l_] := Module[{n = Abs[1/2 (1 - Sqrt[1 + 8*Length@l])]},
   If[IntegerQ@n, 
     SparseArray[Rule[#, #2] & @@@ Thread@{Flatten[Table[{i, j}, {i, n}, {j, i, n}], 1], l}], 
     "Wrong length. The length should be " <>
      ToString[Or @@ ((#[n]*(#[n] + 1)/2) & /@ {Ceiling, Floor})] <> "."]]

Usage:

l = Range@11;
mat@l

Wrong length. The length should be 15 || 10.

l = Range@10;
mat@l

$\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 0 & 5 & 6 & 7 \\ 0 & 0 & 8 & 9 \\ 0 & 0 & 0 & 10 \\ \end{array} \right)$

Your answer only functions when there are exactly 6 elements. But the OP wants a more general solution: "... so for example a list with 36 elements shall form a 8x8 upper triangle matrix." — eldo, Aug 02 '14 at 13:39
@eldo I assumed that you were capable of replacing 3 by 8 ;o) But there you go. — Öskå, Aug 02 '14 at 13:46

John · Answer 3 · 2014-08-02T13:24:44.440

You should try to avoid procedural language in mathematica. I think this should work, but maybe it is not the most efficient:

Code edited for clarity

utMatrix[list_List] := With[{matrixsize = -1/2 + 1/2 Sqrt[1 + 8*Length@list]}, 
PadLeft[Take[list, #], matrixsize, 0] & /@ (Transpose@{Most@#, Rest@# - 1} &
[Accumulate@Join[{1}, Range[matrixsize, 1, -1]]]) 
/;IntegerQ[matrixsize]]

Basically this function partitions the list in sublists of appropriate lengths and then pads them with 0s on the left. The condition at the end checks for lists of wrong lengths.

score 2 · Answer 4 · answered Oct 06 '20 at 13:22

Maybe it's not the most efficient solution, but it's quite simple. I had to fill in the vectors in the specific order.

First, I define a vector, for example:

MatrixDim = 5;
VecLength = (MatrixDim + 1) MatrixDim/2;
InputVector = Table[i, {i, VecLength}];

(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)

And declare a matrix:

MatrixLUp = Table[0 i + 0 j, {i, 1, MatrixDim}, {j, 1, MatrixDim}];

The actual formula that feeds in the matrix is like that:

OldX = 0;
j = 1;
Do[
  i = x - OldX;
  MatrixLUp[[i, j]] = InputVector[[x]];
  If[x == (j + 1) j/2, OldX = x; j++;]
  , {x, 1, VecLength}
];

Finally, the elements in the matrix are shown here:

MatrixLUp//MatrixForm//TeXForm

\begin{array}{ccccc} 1 & 2 & 4 & 7 & 11 \\ 0 & 3 & 5 & 8 & 12 \\ 0 & 0 & 6 & 9 & 13 \\ 0 & 0 & 0 & 10 & 14 \\ 0 & 0 & 0 & 0 & 15 \\ \end{array}

score 1 · Answer 5 · answered Aug 02 '14 at 12:48

toUpperMatrix[l_List] := Module[{i, n, m, k, t},
    n = Length[l];
    m = {};
    k = 1/2 (-1 + Sqrt[1 + 8 n]);
    t = {};
    For[i = 1, i <= n, i++,
        AppendTo[t, l[[i]]];
        If[Length[t] == k,
            AppendTo[m, Join[Table[0, {i, 1, 1/2 (-1 + Sqrt[1 + 8 n]) - k}], t]];
            t = {};
            k--;
        ];
    ];
    Return[m];
];

This is the only method I can figure out. Looking forward to better solutions.

unlikely · Answer 6 · 2014-08-02T14:11:19.780

If you don't care the order you can use the following function:

tpart[list_ /; VectorQ[list] && OddQ[Sqrt[1 + 8 Length[list]]]] := 
 Module[{m = (-1 + Sqrt[1 + 8 Length[list]])/2},
  SparseArray[
   Thread[Flatten[Table[{i, j}, {i, 1, m}, {j, i, m}], 1] -> 
     list], {m, m}]
  ]

For example

tpart[{a1, a2, a3, a4, a5, a6}] // MatrixForm
tpart[Array[a, 36]] // MatrixForm

gives:

Mathematica graphics

If you do care about your order this one (this function is not robust: be sure to pass an appropriately sized list or add a condition):

tpart2[list_] := Module[{m = (-1 + Sqrt[1 + 8 Length[list]])/2, s},
  s = Range[m, 1, -1] //Prepend[1 + Accumulate[#], 1] & //Partition[#, 2, 1] &;
  SparseArray[
   Thread[Array[Band[{1, #}] &, m] -> (Take[list, # - {0, 1}] & /@ s)]
   , {m, m}]
  ]

tpart2[list]
tpart2[list] // MatrixForm
tpart2[list] // Normal

The result is:

Basheer Algohi · Answer 7 · 2014-08-02T14:57:06.723

1

This is if you car about order.

list = {a1, a2, a3, a4, a5, a6, a7, a8, a9, a10};

s = 1/2 (1 + Sqrt[1 + 8 Length@list]);
l = list[[1 + # s - (# (1 + #))/2 ;; (1 + #) s - ((# + 1) (2 + #))/
         2]] & /@ Range[0, s - 2];
SparseArray[Band[{1, #}] -> l[[#]] & /@ Range[Length@l]] // 
  Normal


(* {{a1, a5, a8, a10}, {0, a2, a6, a9}, {0, 0, a3, a7}, {0, 0, 0, a4}}*)

edited Aug 02 '14 at 14:57

answered Aug 02 '14 at 14:39

Basheer Algohi

19,917
1
31
78

eldo · Answer 8 · 2014-08-02T18:50:40.280

1

Inspired by Mr. Wizard's solution this is a certain generalization:

rag[v_, w_] := 
 MapThread[v[[#1 ;; #2]] &, With[{a = Accumulate[w]}, {a - w + 1, a}]]

tri[n_Integer /; n > 0, order_: True, s_Symbol: a] :=
 Module[{x, y},
  x = Range[n, 1, -1];
  y = rag[ToExpression[ToString@s <> # & /@ ToString /@ Range@Total@x], x];
  PadLeft@If[order, Flatten[y, {2}], y]
  ]

tri[3] // MatrixForm

enter image description here

tri[8, False] // MatrixForm

enter image description here

edited Aug 02 '14 at 18:50

answered Aug 02 '14 at 16:30

eldo

67,911
5
60
168

Nice extension. – Mr.Wizard Aug 02 '14 at 18:35

梁國淦 · Answer 9 · 2016-04-22T02:46:44.600

0

If the length of your vector can always be guaranteed to be correct (exactly good for an upper triangular matrix), then the following will work.

v = {a1, a2, a3, a4, a5, a6};
d = (-1 + Sqrt[1 + 8*Length[v]])/2;
Array[If[#1 <= #2, v[[(2*d - #1 + 2)*(#1 - 1)/2 + #2 - #1 + 1]], 0] &, {d,d}]

Please test it yourself and write it into a function if you need to repeatedly use it.

Regards,

Kuo Kan LIANG

edited Apr 22 '16 at 02:46

answered Apr 22 '16 at 02:29

梁國淦

392
1
8

@Shutao, doesn't it depend on the dialect? – J. M.'s missing motivation Apr 22 '16 at 04:17
Sorry guys I have not been wanting to reply to these comments on the spelling of my name, not because I am arrogant, but because I thought it irrelevant to the discussion. – 梁國淦 Apr 26 '16 at 00:59
Actually when I was small and tried to figure out the spelling of my name in English, most people still used old Roman system for spelling non-Latin language pronunciation. There is nothing to fight about this. Why do you care how well the foreigners pronounce your name? It sounds weird anyway. I hope that this is a discussion of knowledge, even if it were not of programming or mathematics. – 梁國淦 Apr 26 '16 at 01:06
@ShutaoTANG To be more precise, 梁國淦 is using Wade–Giles. And, well, with all due respect, if you really care about the standard, then you should be TANG Shutao: http://www.fdcollege.fudan.edu.cn/_upload/article/1e/26/64fb1ac349318df5b653833e8a16/3bc3c4e9-4490-4745-96f8-5dcda875bd51.pdf – xzczd May 08 '16 at 06:02
@xzczd 谢谢你的姓名解释！ – xyz May 09 '16 at 00:49

george2079 · Answer 10 · 2014-08-05T18:42:22.420

0

  n = 6
  vals = Array[a, {n (n + 1)/2}]
  SparseArray[
       SortBy[Tuples[Range[n], {2}] ,
         #[[2]] - #[[1]] &][[-n (n + 1)/2 ;;]] -> vals ] // MatrixForm

enter image description here

without using SparseArray:

 ReplacePart[ConstantArray[0, {n, n}],
      MapThread[#1 -> #2 &, {
         SortBy[Tuples[Range[n], {2}] ,
         #[[2]] - #[[1]] &][[-n (n + 1)/2 ;;]], vals}]] // MatrixForm

edited Aug 05 '14 at 18:42

answered Aug 05 '14 at 18:33

george2079

38,913
1
43
110

Forming an upper triangular matrix from the elements of a list

10 Answers10

Linked