5

I am using operations over Interval and the result of an intersection (or union) contains some singletons. Would it be possible to remove them ?

Example:

Interval[
  {2894486400, 2894486400},
  {2894659200, 2894832000},
  {2895004800, 2895004800},
  {2895177600, 2895350400}
]

Transformed in :

Interval[{2894659200, 2894832000}, {2895177600, 2895350400}]
Mammouth
  • 481
  • 2
  • 9
  • 3
    Try DeleteCases: DeleteCases[%, {$x_, $x_}] – kale Aug 05 '14 at 13:22
  • Works well ! Is the variable $x_ a pattern ? I should learn that type of syntax :) – Mammouth Aug 05 '14 at 13:26
  • 1
    Not necessarily. When matching patterns I just specified a variable x so that the first and last elements in the lists had to be the same. I usually add a $ so I don't get confused if another x has already been defined in my current context. – kale Aug 05 '14 at 13:31
  • Thank you for the precision. I have not seen this very often, do you have any reference (book, article, etc.) that explains this ? – Mammouth Aug 05 '14 at 13:59
  • Nope. Just a personal preference. I do the same thing for functions like FindRoot: $x /. FindRoot[Exp[$x]==5, {$x,1}]. Like I said, complete personal preference. – kale Aug 05 '14 at 14:24

2 Answers2

5

Yes, this is perfectly possible. In fact, there are multiple ways to do this. The most straightforward is to use DeleteCases, as @kale points out in the comments:

interval = Interval[
 {2894486400, 2894486400}, 
 {2894659200, 2894832000}, 
 {2895004800, 2895004800}, 
 {2895177600, 2895350400}
];

DeleteCases[interval, {x_, x_}]

Interval[{2894659200, 2894832000}, {2895177600, 2895350400}]

Here x_ is a named pattern. Because it occurs as {x_, x_}, it only matches those intervals that are singletons.

Another method, my favorite (but probably not as efficient as DeleteCases), is to replace the singletons with Sequence, which get automatically spliced out:

interval /. {x_, x_} -> Sequence[]

Interval[{2894659200, 2894832000}, {2895177600, 2895350400}]
Teake Nutma
  • 5,981
  • 1
  • 25
  • 49
4

For version 10 you might use:

interval ~Select~ DuplicateFreeQ

Interval[{2894659200, 2894832000}, {2895177600, 2895350400}]

For other versions alternatives to DeleteCases include:

Select[interval, UnsameQ @@ # &]

Pick[#, UnsameQ @@@ #] & @ interval

Benchmarks

As requested:

generate[n_] := 
  Sort @ RandomInteger[n, ⌊.7n⌋] ~Partition~ 2 // Apply[Interval];

f1 = DeleteCases[{x_, x_}];
f2 = Select[DuplicateFreeQ];
f3 = Select[UnsameQ @@ # &];
f4 = Pick[#, UnsameQ @@@ #] &;
f5 = # /. {x_, x_} :> Sequence[] &;

Needs["GeneralUtilities`"]

BenchmarkPlot[{f1, f2, f3, f4, f5}, generate, 2^Range[7, 16], "IncludeFits" -> True]

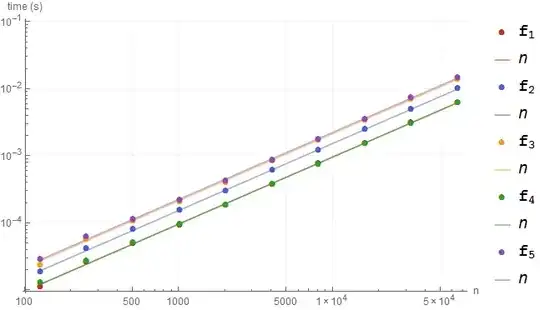
enter image description here

The lines are hard to see here but:

  • f1 and f4 are the winners with nearly identical timings
  • f3 and f5 are the slowest
  • f2 is in the middle
  • All methods have the same complexity, unsurprisingly

If speed is the goal f5 can be improved by using Replace:

f6 = Replace[#, {x_, x_} :> Sequence[], {1}] &; 

BenchmarkPlot[{f1, f5, f6}, generate, 2^Range[7, 16], "IncludeFits" -> True]

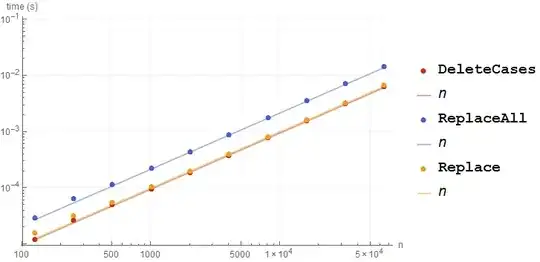
enter image description here

This shows that DeleteCases has only the slightest performance margin over {x_, x_} :> Sequence[] when the latter is used with a targeted levelspec, which I find somewhat surprising as I assumed the latter would incur additional evaluation.

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371