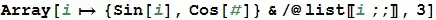Is it possible to specify which range that slot takes from?

Question

consider this example:

list = {a, b, c};
Table[{Sin[i], Cos[j]}, {i, 1, 3}, {j, list[[i ;;]]}]

(*{{{Sin[1], Cos[a]}, {Sin[1], Cos[b]}, {Sin[1], Cos[c]}}, {{Sin[2], 
   Cos[b]}, {Sin[2], Cos[c]}}, {{Sin[3], Cos[c]}}}*)

for the following code:

{Sin[#], Cos[#]} & /@ list[[# ;;]] & /@ {1, 2, 3}

we can get same result if the slot inside Sin (Sin[#]) takes the values from the outer range ({1,2,3})

so in general, is it possible to specify which range that slot takes from?

I read this question twice and I still don't understand it. Edit: Okay, thanks to Verbeia's answer I think I understand. I do find the phrasing of the question confusing. — Mr.Wizard, Aug 05 '14 at 23:21

score 7 · Accepted Answer · answered Aug 05 '14 at 23:01

My first suggestion would be to localize the outer Slot, like this:

With[{indx = #}, {Sin[indx], Cos[#]} & /@ list[[indx ;;]]] & /@  Range[3]

(* {{{Sin[1], Cos[a]}, {Sin[1], Cos[b]}, {Sin[1], Cos[c]}}, {{Sin[2], 
   Cos[b]}, {Sin[2], Cos[c]}}, {{Sin[3], Cos[c]}}} *)

You could also rework the process to get the full set of tuples of {Sin[1],Sin[2],Sin[3]} and {Cos[a],Cos[b],Cos[c]} and keep the ones you want, using something like:

MapThread[#1[[#2 ;;]] &, {Outer[{Sin[#1], Cos[#2]} &, Range[3], list],
   Range[3]}]

score 6 · Answer 2 · answered Aug 05 '14 at 23:37

You can nest Functions to accomplish what I believe you want to:

f = i \[Function] {Sin[i], Cos[#]} & /@ list[[i ;;]];

Array[f, 3] // Column

{{Sin[1],Cos[a]},{Sin[1],Cos[b]},{Sin[1],Cos[c]}}
{{Sin[2],Cos[b]},{Sin[2],Cos[c]}}
{{Sin[3],Cos[c]}}

This looks nicer in the Notebook:

enter image description here

Other methods include:

# /. i_ :> ({Sin[i], Cos[#]} & /@ list[[i ;;]]) & /@ {1, 2, 3}

With[{i = #}, {Sin[i], Cos[#]} & /@ list[[i ;;]]] & /@ {1, 2, 3}  (* Verbeia's *)

Nevertheless I feel that the Table construct is at least as clear as any of these.

score 5 · Answer 3 · answered Aug 06 '14 at 00:33

is it possible to specify which range that slot takes from?

The short answer is "no" (not counting solutions with named arguments since they aren't Slots) but if you really, really want to do it you can write it like I've done below, then #1 refers to the inner Map and #2 refers to the outer Map:

Map[
 Map[
   {Sin[#], Cos[#2]} & @@ # &,
   Thread@{#, list[[# ;;]]}
   ] &,
 {1, 2, 3}
 ]

This technique can be used for more levels I think, so that if you had four Map inside each other you could use #1, #2, #3 and #4 to refer to the different levels. But it isn't worth the trouble to start thinking about it.

Nice. consider this also, {Sin[#1], Cos[#2]} & @@@ Thread[{#, list[[# ;;]]}] & /@ Range[3] — Basheer Algohi, Aug 06 '14 at 00:50

Is it possible to specify which range that slot takes from?

3 Answers3

Linked