Convert a list of rules into 2 lists of integers

Question

If I have a list of n number of rules, what is a concise way of breaking the data into 2 lists of the first and second part of the rule?

This works, but seems like an unnecessary amount of code to me:

data = {
  1 -> 3, 1 -> 3, 1 -> 3, 2 -> 3, 2 -> 3, 2 -> 1, 
  3 -> 2, 3 -> 2, 3 -> 3, 4 -> 1, 4 -> 2, 4 -> 2
};

list1 = First[Partition[Flatten[data /. Rule -> List], 2, 2, 1, {}]~Flatten~{2}]

{1,1,1,2,2,2,3,3,3,4,4,4}

list2 = Last[Partition[Flatten[data /. Rule -> List], 2, 2, 1, {}]~Flatten~{2}]

{3,3,3,3,3,1,2,2,3,1,2,2}

{First[#], Last[#]} & /@ data // Transpose – alancalvitti Aug 06 '14 at 14:18 — alancalvitti, Aug 06 '14 at 14:18
or {list1, list2} = {data[[All, 1]], data[[All, 2]]} – Mike Honeychurch Aug 07 '14 at 00:06 — Mike Honeychurch, Aug 07 '14 at 00:06

score 10 · Accepted Answer · edited May 01 '15 at 06:12

10

This is the shortest I can think of:

{list1, list2} = Transpose[List @@@ data];

list1

{1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4}

list2

{3, 3, 3, 3, 3, 1, 2, 2, 3, 1, 2, 2}

edited May 01 '15 at 06:12

Karsten7

27,448
5
73
134

answered Aug 06 '14 at 15:25

Teake Nutma

5,981
1
25
49

score 9 · Answer 2 · edited Aug 06 '14 at 14:24

9

data[[All, #]] & /@ {1, 2}

{{1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4}, {3, 3, 3, 3, 3, 1, 2, 2, 3, 1, 2, 2}}

edited Aug 06 '14 at 14:24

Öskå

8,587
4
30
49

answered Aug 06 '14 at 14:19

user21

39,710
8
110
167

1

or data[[;; , #]] & /@ {1, 2} to shave off one character. – seismatica Aug 06 '14 at 19:13

Rojo · Answer 3 · 2014-08-06T19:06:45.137

9

data // Query[{Keys, Values}]

or Through@{Keys, Values}@data, or list1=Keys@data; list2=Values@data

edited Aug 06 '14 at 19:06

answered Aug 06 '14 at 18:42

Rojo

42,601
7
96
188

Darn, why didn't I think of that. +1 – Mr.Wizard Aug 06 '14 at 20:49
3

As far as I'm concerned, Through[{Keys,Values}[data]] is the proper answer to this question. +1. Unfortunately, Through is a bit of a weird function. We're discussing a new function called maybe ComposeThrough, giving ComposeThrough[{Keys,Values}, data] in this example (and of course would have an operator form). This would formalize the {op,..} and <|key->op,...|> sugar in Query (and make it faster). – Taliesin Beynon Aug 07 '14 at 18:32
@TaliesinBeynon Sounds great but please also give it a short form (like /@ @* etc.) so that I'll actually use it. By the way I'd still like to chat. Do you have time today? – Mr.Wizard Aug 07 '14 at 20:02
data // Query[{Keys, Values}] doesn't work using version 10.1.0.0. – Karsten7 May 01 '15 at 06:24

score 8 · Answer 4 · edited Apr 13 '17 at 12:55

user21 and Teake Nutma already posted the two methods I use most often. Of these I recommend Part as I believe it will be faster in general. Nevertheless these are hardly the only ways to accomplish this task. First, since the expression produced by List @@@ data will not be packed Thread may be faster than Transpose:

Thread[List @@@ data]

One could also thread over Rule, then replace the outer head with List:

List @@ Thread[data, Rule]

From Undocumented form for Extract we could also use:

Rest @ Extract[data, {{0}, {All, 1}, {All, 2}}]

Benchmarks

A BenchmarkPlot for all methods posted so far.

f1[a_] := a[[All, #]] & /@ {1, 2};
f2 = Transpose[# /. (a_ -> b_) :> {a, b}] &;
f3 = Transpose[List @@@ #] &;
f4 = Thread[List @@@ #] &;
f5 = List @@ Thread[#, Rule] &;
f6 = Rest@Extract[#, {{0}, {All, 1}, {All, 2}}] &;
f7 = Query[{Keys, Values}];
f8 = {Keys@#, Values@#} &

Needs["GeneralUtilities`"]
g[n_] := Rule @@@ RandomInteger[9, {n, 2}];

BenchmarkPlot[{f1, f2, f3, f4, f5, f6, f7, f8}, g, 2^Range[5, 20], "IncludeFits" -> True]

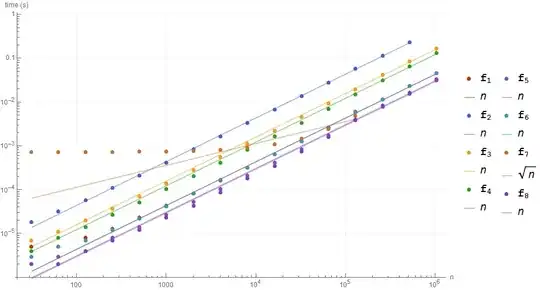(click for larger)

Once again Query has some crazy overhead and should be avoided when performance matters unless inputs are very large.
Keys and Values are very fast when used apart from Query.
List @@ Thread[data, Rule] is as fast as Keys and Values, and faster than Part and Extract which I did not expect.
As expected Thread is slightly faster than Transpose with unpacked data. (f3 and f4)

@TeakeNutma That is quite a bit slower than the present leaders and I'd rather not clutter the graph any further. It is the upper line on this plot: http://i.stack.imgur.com/0gKsU.png compared to f5 and f8. (Ignore the legend.) — Mr.Wizard, Aug 07 '14 at 21:18

RunnyKine · Answer 5 · 2014-08-06T21:00:41.017

4

{#1, #2} & @@@ data // Transpose

{{1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4}, {3, 3, 3, 3, 3, 1, 2, 2, 3, 1, 2, 2}}

edited Aug 06 '14 at 21:00

answered Aug 06 '14 at 20:01

RunnyKine

33,088
3
109
176

gpap · Answer 6 · 2014-08-07T08:43:21.063

2

You can also use HoldPattern:

data /.HoldPattern[a_ -> b_] :> {a, b} // Transpose
{{1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4}, {3, 3, 3, 3, 3, 1, 2, 2, 3, 1, 
  2, 2}}

edited Aug 07 '14 at 08:43

answered Aug 06 '14 at 14:59

gpap

9,707
3
24
66

You can indeed, but it's not necessary to hold the LHS of the rule. data /. (a_ -> b_) -> {a, b} // Transpose or even data /. Rule -> List // Transpose work just as fine. – Teake Nutma Aug 06 '14 at 15:28
yep, you're absolutely right. – gpap Aug 06 '14 at 15:36
@Teake and gpap, you both forgot to localize your pattern names; use :> instead! – Mr.Wizard Aug 06 '14 at 20:51
@Mr.Wizard I claim a typo! – Teake Nutma Aug 06 '14 at 20:54
done! thanks for the comment - this was written as hastily as they come. – gpap Aug 07 '14 at 08:44

Convert a list of rules into 2 lists of integers

6 Answers6

Benchmarks

Related