4

Consider the image below:

GraphData[{"Wheel", 7}]

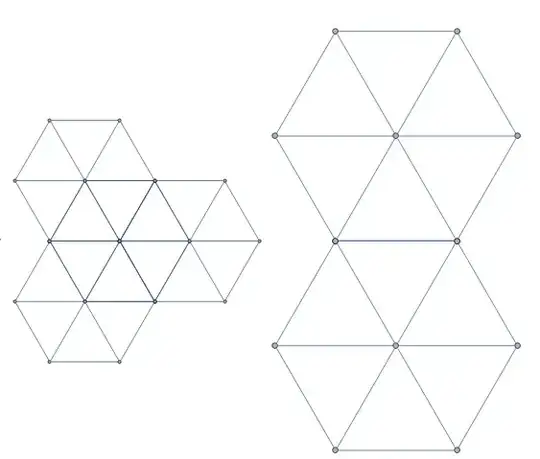
enter image description here

Is it possible in Mathematica to lay several of these Graph along each other and then get the coordinates of the resultant network?

Something like these at the simplest case:

enter image description here enter image description here

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
MOON
  • 3,864
  • 23
  • 49
  • @Öskå I edited the question. – MOON Aug 19 '14 at 10:35
  • @Öskå I did not produce the second and third images in MMA. I just used paint in Windows and made those out of the first image. – MOON Aug 19 '14 at 10:40
  • There is one fundamental problem with this approach based on GraphData: the VertexCoordinates are only given as approximate real numbers, so that the coordinates that you can extract from the Graphics are not the exact geometric values. Basically, I think the information in GraphData is limited to the number of digits that can be visually discerned in a graph display, so you shouldn't use them for high-precision calculations. Not sure why they didn't implement exact values here... – Jens Aug 19 '14 at 23:18

2 Answers2

9

You can get the vertex coordinates, e.g.

g = GraphData[{"Wheel", 7}]
vc=PropertyValue[g, VertexCoordinates]

yielding:

{{-0.5, -0.866}, {0.5, -0.866}, {1., 0.}, {0.5, 0.866}, {-0.5, 
  0.866}, {-1., 0.}, {0., 0.}}

UPDATE

To do the other objects (without the overlaid lines):

grap = GraphicsComplex[vc, Line /@ List @@@ EdgeList[g]];
tr[p_] := GeometricTransformation[grap, TranslationTransform[p]]

First object:

gr1 = Graphics[{grap,
   tr[{1, 0}], tr[{-1/2, -Sin[Pi/3]}], tr[{-1/2, Sin[Pi/3]}]}]

enter image description here

Second object:

gr2 = Graphics[{grap, tr[{0, 2 Sin[Pi/3]}]}]

enter image description here

ubpdqn
  • 60,617
  • 3
  • 59
  • 148
7

Update 3: A one-liner

ClearAll[f];
f[g_, tr : {{_, _} ..}, opts : OptionsPattern[]] := 
             Graphics[Translate[First@Show@g, {{0, 0}, ## & @@ tr}], opts]

g = GraphData[{"Wheel", 7}];
tr1 = {{1, 0}, {-1/2, -Sin[Pi/3]}, {-1/2, Sin[Pi/3]}};
tr2 = {{0, 2 Sin[Pi/3]}};
Row[f[g, #, ImageSize -> 300] & /@ {tr1, tr2}]

enter image description here

Update 2: The simplest approach to convert a Graph g to Graphics turns out to be Show[g] (see this answer by becko -- thanks: @MarkMcClure). So, with translations* defined in previous update:

g = GraphData[{"Wheel", 7}];
g4 = First@Show[g];
g4a = Graphics[Translate[g4, #] & /@ translations1b, ImageSize -> 300];
g4b = Graphics[Translate[g4, #] & /@ translations2b, ImageSize -> 300];
Row[{g4a, g4b}]
(* same pictures as above *)

Update: slightly more streamlined version using Translate and GraphComputation`GraphConvertToGraphics:

g = GraphData[{"Wheel", 7}];
g2 = First@GraphComputation`GraphConvertToGraphics[g];
translations1 = {{1, 0}, {-1/2, -Sin[Pi/3]}, {-1/2, Sin[Pi/3]}};
translations2 = {{0, 2 Sin[Pi/3]}};
translations1b = Prepend[translations1, {{0, 0}}];
translations2b = Prepend[translations2, {{0, 0}}];


g3a = Graphics[Translate[g2, #] & /@ translations1b, ImageSize -> 300];
g3b = Graphics[Translate[g2, #] & /@ translations2b, ImageSize -> 300];
Row[{g3a, g3b}]
(* same pictures as above *)

Original post:

Borrowing the function tr from @ubdqn's excellent answer, and using the undocumented function GraphComputation`GraphConvertToGraphics:

tr2[g_, p_] := GeometricTransformation[g, TranslationTransform[p]];
g2 = First@GraphComputation`GraphConvertToGraphics[g];

g2a = Graphics[{g2, tr2[g2, #] & /@ translations1}, ImageSize -> 300];
g2b = Graphics[{g2, tr2[g2, #] & /@ translations2}, ImageSize -> 300];
Row[{g2a, g2b}]
(* same pictures as above *)
Community
  • 1
kglr
  • 394,356
  • 18
  • 477
  • 896
  • 1
    The GraphComputationGraphConvertToGraphics function is called byShowwhen applied to aGraph. Thus,Show[g]` accomplishes the same thing. – Mark McClure Aug 19 '14 at 14:26
  • @Mark, thank you!! Now that you mention I think I recently saw this cool trick somewhere on this site -- a post/comment by you most probably --, made a mental note to remember, and promptly forgot:) Will you post it as an answer, or should I update this answer? – kglr Aug 19 '14 at 14:32
  • Oh, it's just one tiny little change. I thought about editing your answer but you can do it, if you want. And, yes, I've posted the GraphConvert thing before but more recently learned of the more intuitive approach with Show. – Mark McClure Aug 19 '14 at 14:34
  • @kguler +1 thanks for another useful tool and insight into Show for graphs. – ubpdqn Aug 19 '14 at 22:06
  • @MarkMcClure thanks for commentary and insights...helpful for more complicated graphs. – ubpdqn Aug 19 '14 at 22:09