Mapping data on Archimedes' spiral

Question

I would like to map my data on Archimedes' spiral and preserve the distance between points on the curve. The test data consists of 20 evenly spaced {x,y} coordinates:

data = Table[{i, i}, {i, 20}]

When I map the data to a spiral, the points are not evenly spaced anymore:

Show[ListPlot[{#[[2]] Sin[#[[1]]], #[[2]] Cos[#[[1]]]} & /@ data, 
  AspectRatio -> 1, PlotRange -> {{-20, 20}, {-20, 20}}], 
 ParametricPlot[{t Sin[t], t Cos[t]}, {t, 0, 20}]]

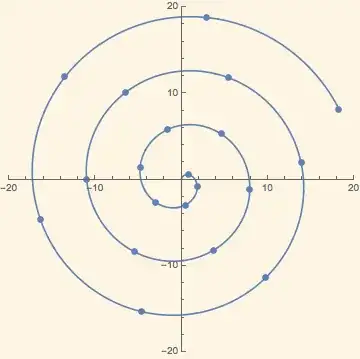
Mathematica graphics

I found this question that links to the algorithm that iteratively generates evenly distributed points on a spiral, but how can I apply this to my set of data points?

The final goal that I'm trying to achieve is to create a function that I can use with ImageTransformation that will remap an image that roughly resembles a line to an Archimedes' spiral.

@Pickett Thanks, I saw this, but again this uses the approach to subdivide a predefined curve. I don't think I can use this because my data will contain noise, and therefore I cannot directly assign my data points to the pre-generated points on a curve. — shrx, Aug 19 '14 at 12:00
Maybe changing your data to Sqrt[2 #] & /@ Table[{i, i}, {i, Range[0, 1/2 20^2, 1/2 20]}] or similar ? — b.gates.you.know.what, Aug 19 '14 at 12:05

score 8 · Accepted Answer · edited Aug 19 '14 at 13:42

8

Using @b.gatessucks' hint, I solved it with the following transformation:

max = Max[data]; 
Show[
  ListPlot[{Sqrt[max #[[2]]] Sin[Sqrt[max #[[1]]]], 
            Sqrt[max #[[2]]] Cos[Sqrt[max #[[1]]]]} & /@ data, 
    AspectRatio -> 1, PlotRange -> {{-20, 20}, {-20, 20}}], 
  ParametricPlot[{t Sin[t], t Cos[t]}, {t, 0, 20}]]

Mathematica graphics

edited Aug 19 '14 at 13:42

m_goldberg

107,779
16
103
257

answered Aug 19 '14 at 12:14

shrx

7,807
2
22
55

score 4 · Answer 2 · edited Apr 13 '17 at 12:56

4

Borrowing from Szcabolcs' answer here:

Off[FunctionInterpolation::ncvb]

PointsOnCurve[fun_, lim_, points_] :=

 Module[{arclength, curvepoints},

  arclength = 
   Derivative[-1][FunctionInterpolation[Evaluate @ Norm @ D[fun, t], {t, 0, lim}]];

  curvepoints = fun /. t -> # & /@
      Table[InverseFunction[arclength][x], {x, 0, #, # / points}] & [arclength[lim]];

  Show[
   ParametricPlot[fun, {t, 0, lim}],
   Graphics[{Red, PointSize[0.02], Point[curvepoints]}]]]

PointsOnCurve[{t Sin[t], t Cos[t]}, 20, 30]

enter image description here

PointsOnCurve[{Cos[t], Sin[2 t]}, 2 Pi, 30]

enter image description here

edited Apr 13 '17 at 12:56

Community

1

answered Aug 19 '14 at 12:14

eldo

67,911
5
60
168

You use the variable points twice, as number of points, and as a points list – hieron Aug 19 '14 at 13:05
@hieron Thanks, very attentive, I changed the answer – eldo Aug 19 '14 at 13:13
Switching off the message is not needed if you define spiral SetDelayed, which simplifies also the spiralpoints expression. – hieron Aug 19 '14 at 13:52
1

I am not looking for a function to generate the points, I want to remap the points that I will obtain experimentally. – shrx Aug 19 '14 at 15:03

Mapping data on Archimedes' spiral

2 Answers2