How to count the integer grid numbers defined by inequalities?

Question

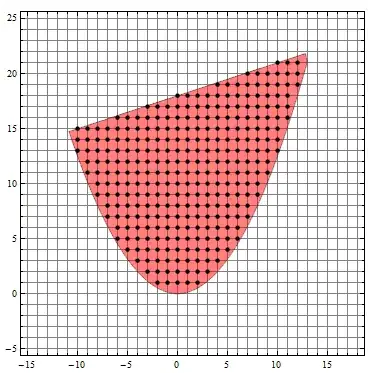
I have the following code to show a red area defined by inequalities:

ClearAll["Global`*"];
p = Reduce[y <= 3/10 x + 18 && y > x^2/8, {x, y}]
r = RegionPlot[p, {x, -15, 18}, {y, -5, 25}, 
   GridLines -> {Table[i, {i, -15, 18}], Table[j, {j, -5, 25}]}, 
   PlotStyle -> Directive[{Opacity[0.5], Red}]];
bg = Graphics[{Opacity[0.2], Yellow, Rectangle[{-16, -6}, {19, 26}]}];
range = First /@ 
  Differences /@ (PlotRange /. Options[r]); target = 1; Show[{r, bg}, 
 AspectRatio -> (Last[range]/First[range]/target)]

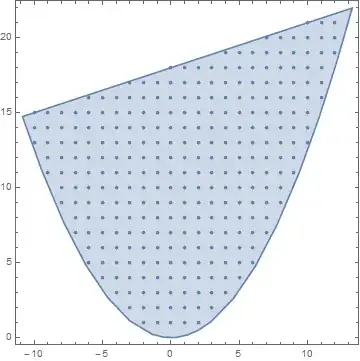
which shows:

enter image description here

How can I count those integer grids and highlight them with colored dots?

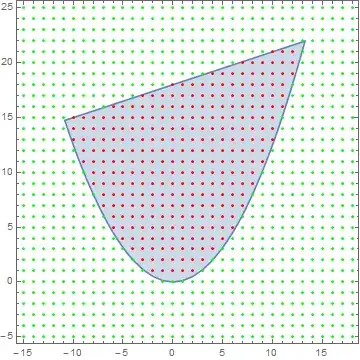
Closely related: How to find lattice points on a line segment?. If there are many solutions Reduce can't be efficient however a neat approach with FrobeniusSolve can yield all interesting solutions as in one of the answers in the link. For benchmarks see this answer Finding the number of solutions to a diophantine equation. — Artes, Aug 22 '14 at 13:02
@Artes Those links show efficient methods, as such problems go. But they require polytope regions (i.e. linear inequalities). — Daniel Lichtblau, Aug 22 '14 at 13:18

b.gates.you.know.what · Accepted Answer · 2014-08-22T12:56:55.220

9

You can do :

p = ImplicitRegion[y <= 3/10 x + 18 && y > x^2/8, {x, y}]

points = Reduce[Element[{x, y}, p], {x, y}, Integers]

pp = Cases[points, x == xx_ && y == yy_ -> {xx, yy}]

pp // Length
(* 286 *) 

Show[RegionPlot[p], ListPlot[pp]]

enter image description here

edited Aug 22 '14 at 12:56

answered Aug 22 '14 at 12:50

b.gates.you.know.what

20,103
2
43
84

1

You can directly to pp using Reduce with pp = {x, y} /. {Reduce[Element[{x, y}, p], {x, y}, Integers] // ToRules}; – Bob Hanlon Aug 22 '14 at 14:56
@BobHanlon Thanks, I knew there must have been a better way. – b.gates.you.know.what Aug 22 '14 at 15:07

kglr · Answer 2 · 2014-08-22T15:35:29.003

8

eqn = y <= 3/10 x + 18 && y > x^2/8;
sol = Reduce[eqn, {x, y}, Integers];
Length @ sol
(* 286 *)
points = {x, y} /. {ToRules[sol]}; (* thanks: BobHanlon *)
RegionPlot[eqn, {x, -15, 18}, {y, -5, 25}, 
           GridLines -> {Range[-15, 18], Range[-5, 25]}, 
           PlotStyle -> Directive[{Opacity[0.5], Red}], 
           Epilog -> {PointSize[Medium], Point[points]}]

enter image description here

edited Aug 22 '14 at 15:35

answered Aug 22 '14 at 13:03

kglr

394,356
18
477
896

You can go directly to points using Reduce with points = {x, y} /. {Reduce[eqn, {x, y}, Integers] // ToRules}; – Bob Hanlon Aug 22 '14 at 15:03
@BobHanlon, thank you; will update with you suggestion. – kglr Aug 22 '14 at 15:32

RunnyKine · Answer 3 · 2014-08-22T15:46:15.337

Here is another solution using V10 functionalities:

region = ImplicitRegion[y <= 3/10 x + 18 && y > x^2/8, {{x, -15, 18}, {y, -5, 25}}];

lis = Tuples[{Range[-15, 18], Range[-5, 25]}];

We create a RegionMemberFunction

rm = RegionMember[region];

Now we select from lis the points that are in the region:

in = Select[lis, rm];

Length @ in

286

Visualize:

out = Complement[lis, in];

Show[RegionPlot[region], Graphics[{Red, Point[in],Green, Point[out]}], 
                         PlotRange -> {{-15, 18}, {-5, 25}}]

Mathematica graphics

How to count the integer grid numbers defined by inequalities?

3 Answers3