I need to solve this Fredholm integral equation of the second kind:
f[s]+integrate[f[t] K[s,t],{t,0,1}]=s
where 0<=s<=1.
The kernel is:
K[s,t]=(a/2)*(BesselJ[1,a*(s+t)]-BesselJ[1,a*Abs[s-t]]-i*StruveH[1,a*(s+t)]+i*StruveH[1,a*Abs(s-t)])
where a: real, i: imaginary unit.
I tried to solve this with the method described here: Integral equation numerical solution with NDSolve, this is the best algorithm for this case I have come across so far but it takes for ages and in the end it doesn't produce any result (due to memory insufficiency). Could anyone please help me solve it?
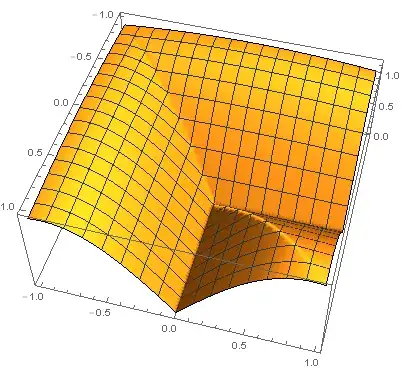
Awill not fit here. – PlatoManiac Aug 26 '14 at 17:26Plot3D[Kpart[s, t],{s,-1,1},{t,-1,1},PlotPoints-> 40]to plot the kernel. – PlatoManiac Aug 27 '14 at 11:12