6

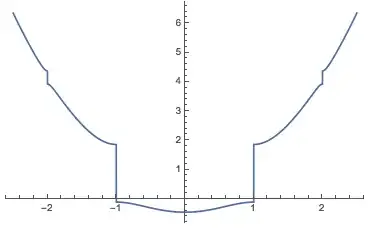
Consider the MathieuCharacteristicA function, which is a piecewise function according to the documentation. The discontinuity happens at integer number.

With[{V0 = -1}, 
 Plot[MathieuCharacteristicA[κ, V0], {κ, -2.5, 2.5}]]

enter image description here

Consider the point approaching k=2 from the left side , and plot the Mathieu funtions near that point. 

ParallelTable[
 Plot[Evaluate@
   With[{V0 = -1, κ = 2 - ϵ}, 
    Re@MathieuC[MathieuCharacteristicA[κ, V0], V0, 
      z]], {z, -10, 10}, PlotRange -> All, 
  ImageSize -> Medium], {ϵ, {10^-8, 15/10*10^-8, 18/10*10^-8,
    2*10^-8}}]

enter image description here

We see that from points k=2-10^-8 , k=2-1.5*10^-8 to points k=1.8*^-8, k=2*^-8, there are big discontinouity. Why does this big discontinuity happen in the Mathieu function, even we are still away from the piecewise point? Which result is correct?

Moreover, as I increase the working precision, the results changes. Which results should I trust?

ParallelTable[
 Plot[Evaluate@
   With[{V0 = -1, κ = 2 - ϵ}, 
    Re@MathieuC[MathieuCharacteristicA[κ, V0], V0, 
      z]], {z, -10, 10}, PlotRange -> All, ImageSize -> Medium, 
  WorkingPrecision -> 50], {ϵ, {10^-8, 15/10*10^-8, 
   18/10*10^-8, 2*10^-8}}]

enter image description here

Update:

More strange behavior

NLimit[
 Re@MathieuC[MathieuCharacteristicA[κ, -1], -1, 
   0], κ -> 2, Direction -> 1, WorkingPrecision -> 100]
(*
 0.000026560352729499428275267693547091828644960849846890155742135607985075453865741662994877041
*)


N[
 Table[Re@MathieuC[MathieuCharacteristicA[2 - ϵ, -1], -1, 
    0], {ϵ, {10^-6, 10^-8, 10^-10, 10^-20, 10^-40, 10^-60, 
    10^-100}}], 100]
(* \
{9.375519741470728355592491183508603286638427801561870220416306315833951776806837902179623867179198570*10^-6, 
 9.375519742493871990285719573456924995106820123921565403331967009687923231481580841077469030562191305*10^-8, 
 9.375519742493974304649207591451232553957148872416907065490732452953108780592926489536671069329119067*10^-10, 
 9.375519742493974314881667185336397875216528878100913700967589255793432748631135267810942389900367393*10^-20, 
 9.375519654864253585910474819580416042344587293945440367769556457939085038181962308922619162634748808*10^-40,
1.114388591781733115021002428520876171768008184684161143978162399223107768160400228809114697590700165,
1.114388591781733115021002428520876171768008184684161143978162399223107768160400228809114697590700165} *)

What's the correct limit for k->2 ?

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
xslittlegrass
  • 27,549
  • 9
  • 97
  • 186

1 Answers1

5

If we compare N on the exact values with the MachinePrecision values, we see that the second two graphs (of the first quartet) look correct and the first two are wrong.

Block[{z = 0},
 Table[With[{V0 = -1, κ = 2 - ϵ}, 
   Re@MathieuC[MathieuCharacteristicA[κ, V0], V0, z]], {ϵ, {15/10*10^-8, 18/10*10^-8}}]
 ]
N[%, 6]
(*
{MathieuC[MathieuCharacteristicA[399999997/200000000, -1], -1, 0], 
 MathieuC[MathieuCharacteristicA[999999991/500000000, -1], -1, 0]}

{1.4063279613740616126811177594156`6.*^-7, 1.6875935536488557009743434482017`6.*^-7} 
*)

Block[{z = 0.},
 Table[With[{V0 = -1, κ = 2 - ϵ}, 
   Re@MathieuC[MathieuCharacteristicA[κ, V0], V0, z]], {ϵ, {15/10*10^-8, 18/10*10^-8}}]
 ]
(*
{1.11439, 1.7027*10^-7}
*)

As the OP showed, this can be seen in the plots, if the WorkingPrecision is set high enough. Clearly, one should trust the second quartet of plots if one is going to trust Mathematica at all. N[expr, n] will report the answer with a precision that is supposed to be correct.

Edit

As @acl has observed Mathieu functions are difficult functions numerically. I would expect it to be even more difficult near a singular point of MathieuCharacteristicA[κ, -1], where a little round-off error causes a discontinuous jump.

The following seem entirely consistent with the left-hand limit being zero, which is at the same time not inconsistent with the OP's evaluation of NLimit.

N@Block[{$MaxExtraPrecision = 500},
  NLimit[Re@MathieuC[MathieuCharacteristicA[κ, -1], -1, 0],
    κ -> 2, Direction -> 1, WorkingPrecision -> 300, Terms -> 50]
  ]

N[Re@MathieuC[MathieuCharacteristicA[2, -1], -1, 0], 10]

N@Block[{$MaxExtraPrecision = 500},
  NLimit[Re@MathieuC[MathieuCharacteristicA[κ, -1], -1, 0],
    κ -> 2, Direction -> -1, WorkingPrecision -> 300, Terms -> 50]
  ]
(*
-1.49047*10^-45
0.8157268391
1.15361
*)

The inconsistencies observed by the OP seem to be due to round-off error. I suppose one complaint is that Mathematica issues no warnings in evaluating the OP's examples, especially the ones involving N applied to an exact value.

Community
  • 1
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Why does this big discontinuity happen in the Mathieu function, even we are still away from the piecewise point? You think Mathematica just got wrong? – xslittlegrass Aug 27 '14 at 17:52
  • @xslittlegrass Round-off error, no? (Perhaps I should point it out explicitly?) – Michael E2 Aug 27 '14 at 17:56
  • I'm not convinced it's simply the round-off error, see my updates. – xslittlegrass Aug 27 '14 at 19:57
  • 1
    @xslittlegrass Try Block[{$MaxExtraPrecision = 500}, N[Table[Re@MathieuC[MathieuCharacteristicA[2 - \[Epsilon], -1], -1, 0], {\[Epsilon], {10^-6, 10^-8, 10^-10, 10^-20, 10^-40, 10^-60, 10^-100}}], 300]] (I wouldn't think 100 digits was enough for 2 - 10^-100, which requires 101 digits just for itself.) – Michael E2 Aug 27 '14 at 20:03
  • What about the disagreement to NLimit? – xslittlegrass Aug 27 '14 at 20:14
  • 1
    @xslittlegrass What calculations does NLimit actually do? – Michael E2 Aug 27 '14 at 20:28
  • NLimit "numerically finds the limiting value of expr as z approaches Subscript[z, 0]." – xslittlegrass Aug 28 '14 at 01:25
  • @xslittlegrass Yes, but how? What calculations does it do? You need to know that in order to understand what's going on. – Michael E2 Aug 28 '14 at 01:30
  • Sorry I still don't get you. But I see you use Terms options. But if you increase upto 100 terms, you get inconsistent result again. N@Block[{$MaxExtraPrecision = 500}, NLimit[Re@ MathieuC[MathieuCharacteristicA[\[Kappa], -1], -1, 0], \[Kappa] -> 2, Direction -> 1, WorkingPrecision -> 300, Terms -> 100]] (*1.11439*) – xslittlegrass Aug 28 '14 at 02:27
  • @xslittlegrass What terms did NLimit add? If they were closer to κ = 2, then you will have to increase the precision more to avoid the round-off error. In other words, the closer to the singularity at 2 you push the calculation, the greater the precision you will need to get an accurate result. – Michael E2 Aug 28 '14 at 02:30
  • OK, I start to see your point. Thanks for the help :) – xslittlegrass Aug 28 '14 at 02:38