14

I've a list of rectangles in the form

{index, {centerX, centerY}, {width, height}}

I want to find intersecting rectangles list. I want to obtain a list on the form

{{indx...indy},{indt...indz}...}

Every element of this list is a list of rectangles that have at least an intersection in common, with transitive property: if rectangle 1 intersects rectangle 2 that intersect rectangle 3, these are a part of the same group.

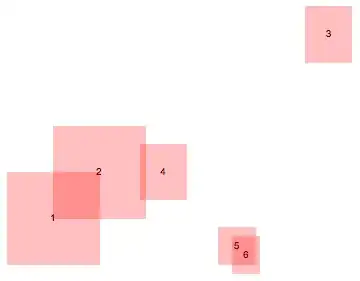
If I've this situation in the image below, my intersecting list should be

{{1,2,10},{6},{7,5},{3},{4,8,9}}

(element order is not important). How can I accomplish this?

enter image description here

EDIT: There's a real sample data, with two groups and an isolated rectangle:

obj2 = {
   {1, {0, 0}, {1, 1}},
   {2, {0.5, 0.5}, {1, 1}},
   {3, {3, 2}, {0.5, 0.6}},
   {4, {1.2, 0.5}, {0.5, 0.6}},
   {5, {2, -0.3}, {0.4, 0.4}},
   {6, {2.1, -0.4}, {0.3, 0.4}}
   };
Jepessen
  • 950
  • 6
  • 16

4 Answers4

17

Here is a graph theory approach:

ids = obj2[[All, 1]];
idToRectangleRules = #1 -> Rectangle[#2 - #3/2, #2 + #3/2] & @@@ obj2;

intersectingIdPairs = Select[
  Subsets[ids, {2}],
  Area @ RegionIntersection[# /. idToRectangleRules] > 0 &
];

overlappingIdGroups = ConnectedComponents @ Graph[ids, intersectingIdPairs]

{{1, 2, 4}, {5, 6}, {3}}

Visualizing:

Graphics @ {
  { Opacity[0.5], Pink, Values @ idToRectangleRules },
  { Text[#1, RegionCentroid @ #2 ] & @@@ idToRectangleRules }
}

enter image description here

Teake Nutma
  • 5,981
  • 1
  • 25
  • 49
ubpdqn
  • 60,617
  • 3
  • 59
  • 148
  • Thanks. I was alsto trying to think it as graph problem but I didn't know how to handle it... – Jepessen Sep 05 '14 at 12:21
  • +1 This is much faster than my answer, especially when the number of rectangles grows. – Teake Nutma Sep 05 '14 at 12:42
  • I took the liberty to refactor your code -- if it's not to your liking please rollback the edit. – Teake Nutma Sep 05 '14 at 14:08
  • @TeakeNutma thank you for edit. It is an improvement, so no need to rollback. – ubpdqn Sep 05 '14 at 14:13
  • While this is already quite fast, it would be much faster still if Area @ RegionIntersection is replaced with a simple function that checks the bounds of the rectangles. (On my machine that's roughly 10^3 times faster). – Teake Nutma Sep 05 '14 at 18:00
13

Let's first convert the input data to rectangles:

ToRectangle[{id_, center_, dimensions_}] := 
  {{id}, Rectangle[center - dimensions/2, center + dimensions/2]};

rectangles = ToRectangle /@ obj2;

Check if we have two groups and one isolated rectangle:

Graphics @ {
  {Text @@@ obj2},
  {Red, Opacity[1/4], Rest /@ rectangles}
}

Mathematica graphics

Ok, good. Let's combine the regions:

CombineRegions[regions_List] :=
  First /@ FixedPoint[
    Replace[
       #,
       {before___, {id1_, region1_}, inbetween___, {id2_, region2_}, after___} 
          /; Area @ RegionIntersection[region1, region2] > 0 
          :> {before, inbetween, after, {Join[id1, id2], RegionUnion[region1, region2]}}
    ] &,
    regions
  ];

CombineRegions @ rectangles

 {{3}, {4, 1, 2}, {5, 6}}

While this produces the correct answer, it becomes quite slow when the number of rectangles grows. This is due to the pattern matcher restarting from the first position after each replacement, which causes a lot of redundant calls to Area @ RegionIntersection[region1, region2] (which is already quite slow in itself).

For large number of rectangles ubpdqn's answer is much faster.

Community
  • 1
Teake Nutma
  • 5,981
  • 1
  • 25
  • 49
  • very nice +1...I clearly misinterpreted the rectangles – ubpdqn Sep 05 '14 at 12:16
  • Thanks a lot. This is exactly what I needed. – Jepessen Sep 05 '14 at 12:20
  • +1, in this case ReplaceRepeated can also be used instead of FixedPoint[Replace.... – C. E. Sep 05 '14 at 13:28
  • @Pickett I deliberately avoided ReplaceRepeated because Rectangle also comes with a list of two elements, and I wanted to make sure the whole expression got replaced instead of a subexpression. – Teake Nutma Sep 05 '14 at 13:41
  • @TeakeNutma Given the level of your answers I figured you had a reason for it, but I still think it works in this particular case. The pattern of the rectangle is Rectangle[{min,max},{min,max}] and it can't match your pattern which is {{el1,el2},{el3,el4}}. It would be different if the pattern for a rectangle was Rectangle[{{min,max},{min,max}}]. Anyway it doesn't matter. Even if it was done just to be on the safe side it's, that's a viable reason too. – C. E. Sep 05 '14 at 13:51
8

A method using the FindClusters function with a custom DistanceFunction:

distFunc =
   Function[{rect1, rect2},
            Block[{cpt1 = rect1[[2]], cpt2 = rect2[[2]],
                   dim1 = rect1[[3]]/2, dim2 = rect2[[3]]/2,
                   corners},
                  corners = cpt2 - cpt1 + # & /@
                              Flatten[
                                      Outer[List, {-1, 1} dim2[[1]], {-1, 1} dim2[[2]]],
                                      1] // Abs;
                  If[Or @@ (#1 < dim1[[1]] && #2 < dim1[[2]] & @@@ corners),
                     0, 1]
                 ]
           ];

FindClusters[obj2, DistanceFunction -> distFunc]

{
   {
    {1, {0, 0}, {1, 1}}, 
    {2, {0.5, 0.5}, {1, 1}}, 
    {4, {1.2, 0.5}, {0.5, 0.6}}
   }, 
   {
    {3, {3, 2}, {0.5, 0.6}}
   }, 
   {
    {5, {2, -0.3}, {0.4, 0.4}}, 
    {6, {2.1, -0.4}, {0.3, 0.4}}
   }
  }
Silvia
  • 27,556
  • 3
  • 84
  • 164
  • +1. This is nice because it can works also with Mathematica versions less than 10 in which RegionIntersection and RegionMeasure are defined. – Jepessen Sep 08 '14 at 07:59
  • @Jepessen Thanks. Working for version<10 is exactly the point :) – Silvia Sep 09 '14 at 08:37
6

Here is a somewhat quirky way using graph operations to perform the transitive closure.

(* object descriptors *)
obj = 
  {{1, {0, 0}, {1, 1}}, {2, {0.5, 0.5}, {1, 1}}, {3, {3, 2}, {0.5,0.6}}, {4, {1.2, 0.5}, 
   {0.5, 0.6}}, {5, {2, -0.3}, {0.4, 0.4}}, {6, {2.1, -0.4}, {0.3, 0.4}}};

toRect[{, {cx, cy_}, {w_, h_}}] :=
  Rectangle[{cx - w/2, cy - h/2}, {cx + w/2, cy + h/2}]


(* taking care to avoid converting each descriptor to a rectangle more than once *)
intersects =
  Select[
    Subsets[{#[[1]], toRect[#]} & /@ obj, {2}], 
    RegionMeasure[RegionIntersection[#[[1, 2]], #[[2, 2]]]] > 0 &
  ][[All, All, 1]]

{{1, 2}, {2, 4}, {5, 6}}

connected = 
  ConnectedComponents[TransitiveReductionGraph[Graph[UndirectedEdge @@@ intersects]]]

{{1, 2, 4}, {5, 6}}

singletons = Complement[{#} & /@ Range@Length @ obj , {#} & /@ Flatten[intersects]]

{{3}}

Join[connected, singletons]

{{1, 2, 4}, {5, 6}, {3}}

Update

Öskå wants me to show the rectangles, so here they are.

toText[{indx_, cntr : {_, _}, _}] := Text[Style[indx, 18], cntr]

Graphics[{{Opacity[.4], toRect[#]} & /@ #, {White, toText[#]} & /@ #} & @ obj]

rects

Community
  • 1
m_goldberg
  • 107,779
  • 16
  • 103
  • 257
  • @Öskå. I don't see any bracketing problem. I can draw the rectangles, but they will be the same as seen ubpdqn's answer. Do you still think I show them? – m_goldberg Sep 05 '14 at 15:05
  • 2
    Could you elaborate a bit on the advantage of using TransitiveReductionGraph instead of directly Graph[vertices, edges]? – Teake Nutma Sep 05 '14 at 17:58
  • @TeakeNutma. I'm not sure I understand what you are asking. The OP asked for the transitive closure. TransitiveReductionGraph seemed an easy way to compute it. – m_goldberg Sep 05 '14 at 23:05
  • 1
    Well, it's not as simple as ubpdqn's approach which gets the transitive closure more directly. So using TransitiveReductionGraph looks a bit redundant, and I was wondering whether it has e.g. speed benefits. – Teake Nutma Sep 06 '14 at 07:51
  • 1
    @TeakeNutma. Do not claim any speed benefits. I just thought it was an interesting variant that people might want to aware of. – m_goldberg Sep 06 '14 at 09:54
  • Indeed TransitiveReductionGraph seems to be unnecessary. Dropping it should make no difference. – Szabolcs Feb 19 '18 at 20:32