How to generate a blank crossword sheet?

Question

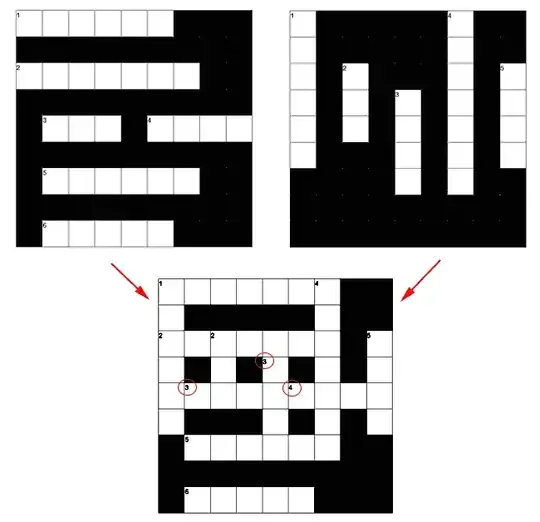
I attempted to generate a blank crossword sheet. My method is by combining the rows and columns as shown on the graph below. However, some of the across and down numbers then appeared out of place after combining. What is the better way to obtain a blank crossword sheet?

enter image description here

fillRow[i_] := (
   startPos = RandomInteger[{1, randomStartPos}] ;
   randomWordLen = RandomInteger[{minWordLen, dimX - startPos}];
   endPos = startPos + randomWordLen - 1;
   Do[cwSheet[[i, n]] = 0, {n, startPos, endPos}];
   AppendTo[ hintNumPad, { counter++, {startPos, dimX - i}}]
    If[endPos <= dimX/2,
     randomWordLen = RandomInteger[{minWordLen, dimX - endPos - 1}];
     Do[cwSheet[[i, n]] = 0, {n, dimX, dimX - randomWordLen + 1, -1}];
     AppendTo[ 
      hintNumPad, { counter++, {dimX - randomWordLen + 1, dimX - i}}];
     ]
   );


fillCol[j_] := (
   startPos = RandomInteger[{1, randomStartPos}] ;
   randomWordLen = RandomInteger[{minWordLen, dimY - startPos}];
   endPos = startPos + randomWordLen - 1;
   Do[cwSheet[[   n , j]] = 0, {n, startPos, endPos}];
   AppendTo[ hintNumPad, { counter++, { j, dimY - startPos  }}]
     If[endPos <= dimX/2,
     randomWordLen = RandomInteger[{minWordLen, dimX - endPos - 1}];
     Do[cwSheet[[n, j]] = 0, {n, dimY, dimY - randomWordLen + 1, -1}];
     AppendTo[ hintNumPad, { counter++, {j, randomWordLen - 1  }}];
     ] 
   );

minWordLen = 3;
hintNumPad = {};
{dimX, dimY} = {9, 9};
randomStartPos = 4;
Clear[cwSheet];

cwSheet = ConstantArray[1, {dimX, dimY}];

 counter = 1;
 Do[fillRow[k], {k, 1, dimY, 2}]; 

 counter = 1;
 Do[fillCol[k], {k, 1, dimX, 2}]; 


g = MatrixPlot[cwSheet , Mesh -> All,
  Frame -> False,
  ColorFunction -> "Monochrome", 
  Epilog -> {Text[Style[#[[1]], 9], #[[2]] + {-0.9, 0.8}] & /@ 
     hintNumPad}]

The correct positions of the hint numbers should look like this:

enter image description here

They look in-place to me, given the original rows and columns; seems like you need to tweak the algorithm that generates the original rows and columns themselves. — Andrew Cheong, Sep 06 '14 at 03:09
It looks entirely wrong to me, even after the movements of numbers indicated in your final drawing. In crosswords I am familiar with (UK, occasionally US) there would be a 2 where you have 4 in the first row, a 3 where you have 2 in the first column, 4 where you have 2 in the third column, etc. Perhaps number the solution spaces after assembling the grid ? — High Performance Mark, Sep 06 '14 at 10:46

ybeltukov · Accepted Answer · 2014-09-06T14:41:58.267

One can use CellularAutomaton and apply only one rule: do not allow 4 white cells together!

ClearAll[f];
f@{{1, 1, _}, {1, _, _}, {_, _, _}} = 0;
f@{{_, 1, 1}, {_, _, 1}, {_, _, _}} = 0;
f@{{_, _, _}, {_, _, 1}, {_, 1, 1}} = 0;
f@{{_, _, _}, {1, _, _}, {1, 1, _}} = 0;
f@{_, {_, x_, _}, _} := If[Random[] < 0.1, 1, x];

Here 0 and 1 mark black and white cells respectively. These rules are so simple so we have to introduce an enhancement: delete words of length 2 and select large morphological components.

del = # //. {x___, 0, 1, 1, 0, z___} :> {x, 0, 0, 0, 0, z} &;

ca = Unitize@SelectComponents[#, Large] &@
          MorphologicalComponents[#, CornerNeighbors -> False] &@
        ArrayPad[#, -1] &@del@Transpose@del@ArrayPad[#, 1] &@
    CellularAutomaton[{f[#] &, {}, {1, 1}}, #, {{200}}][[1]] &;

Now we can apply ca several times to obtain better result

res = Nest[ca, ConstantArray[0, {12, 12}], 4];

It remains to find labels and show the result

labels = Position[#, {_, {0, 1, 1}, _} | {{_, 0, _}, {_, 1, _}, {_, 1, _}},
    {2}] &@Partition[#, {3, 3}, 1] &@ ArrayPad[res, 1];

ArrayPlot[1 - res, Mesh -> All, Frame -> False, MeshStyle -> Black, 
 Epilog -> MapIndexed[Text[Style[#2[[1]], 9], 
   {#[[2]] - 0.95, Length@res - #[[1]] + 0.95}, {-1, 1}] &, labels]]

enter image description here

P.S. There is a small probability to obtain incorrect field.

CellularAutomaton apply rules with periodic boundary conditions. One can treat it as the torus topology of the crossword (code):

enter image description here

Thank you so much. To tell the true, looking at your code, Mathematica suddenly became a complete foreign language to me! :) — Putterboy, Sep 06 '14 at 13:31
@Putterboy It was the same for me two years ago. There is a nice guide: What the @#%^&*?! do all those funny signs mean?. — ybeltukov, Sep 06 '14 at 13:40
@ybeltukov +1 thanks for a this very instructive post and creative use of cellular automata, particularly nice to have random component and constraint word length > 2. — ubpdqn, Sep 07 '14 at 01:20

Dr. belisarius · Answer 2 · 2014-09-12T19:09:25.087

9

By Using HitMissTransform[] to detect "words" of length > 1

(*Generate a symmetric Puzzle**)
n = 15;
f = Unitize@(# + Transpose@#) &;
i = f@BlockRandom[RandomChoice[{0, 1}, {n, n}]];

(*Calculate*)
k = {{-1, 1, 1}};
p = Position[f@ImageData@HitMissTransform[Image@i, k, Padding -> 0], 1];

(* Print *)
ArrayPlot[i - 1, Mesh -> All, 
  Epilog -> MapIndexed[Text[#2[[1]],#1] &, SortBy[p/.{a_,b_}:>{b -.8, n-a +.8}, -#[[2]] &]]]

Mathematica graphics

edited Sep 12 '14 at 19:09

answered Sep 06 '14 at 23:39

Dr. belisarius

115,881
13
203
453

1

+1 Mathematica has function for everything :) – ybeltukov Sep 07 '14 at 06:20

score 4 · Answer 3 · answered Sep 07 '14 at 01:14

The following generates square crosswords. It has a number of limitations.

cw[rv_] :=
 Module[{lg, sa, val, a, d, i, sel, text},
  lg = Length[rv[[1]]];
  sa = SparseArray[rv];
  val = Complement[Tuples[Range[lg], 2], sa["NonzeroPositions"]];
  a[list_, x_] := And[Not[MemberQ[list, x + {0, -1}]],
    MemberQ[list, x + {0, 1}]
    ];
  d[list_, x_] := 
   And[Not[MemberQ[list, x + {-1, 0}]], MemberQ[list, x + {1, 0}]];
  i[list_, x_] := 
   And @@ (Not@MemberQ[list, x + #] & /@ {{-1, 0}, {1, 
        0}, {0, -1}, {0, 1}});
  sel = Select[val, Or[a[val, #], d[val, #], i[val, #]] &];
  text = MapIndexed[
    Text[First@#2, {Last@#1, lg - First@#1} - {0.8, -0.8}] &, sel];
  ArrayPlot[rv, Mesh -> All, Epilog -> text]]

Examples:

anim = cw[RandomVariate[BernoulliDistribution[0.4], #]] & /@ {{4, 
     4}, {5, 5}, {6, 6}, {7, 7}, {8, 8}, {9, 9}, {10, 10}};

enter image description here

or static version:

enter image description here

If you happened to have your square crossword, e.g. this rather uninspiring one:

mat = {{0, "C", "R", "O", "S", "S", 0},
   {0, "A", 0, 0, "E", 0, "H"},
   {0, "N", "O", "T", "E", 0, "E"},
   {0, 0, 0, 0, 0, 0, "L"},
   {"T", "O", "E", 0, "H", "O", "P"},
   {"A", 0, "R", 0, "A", 0, "S"},
   {"P", "L", "A", "N", "T", 0, 0}
   };
cw[mat /. {_String :> 0, 0 -> 1}]
Show[cw[mat /. {_String :> 0, 0 -> 1}], 
 Graphics@Text[
     Style[Extract[mat, #], Red, 
      20], {Last@#, 7 - First@#} + {-0.5, 0.5}] & /@ (SparseArray[
     mat]["NonzeroPositions"])]

enter image description here

How to generate a blank crossword sheet?

3 Answers3