1

I am fairly new to Mathematica, but I am trying to plot an orbit of the Earth around the sun using the equation:

$\quad r(t+dt) = (2 - G*M*dt^2/r^3)*r(t) - r(t-dt)$

I need to break this into components and give Earth an initial velocity. Essentially my goal is to write the code similar to the way I might write it in Fortran but make use of the plotting functions that Mathematica has.

This is a homework assignment so unfortunately I do actually need to do it in this basic Fortran style.

Can anyone point me in the right direction?

Karl
  • 375
  • 1
  • 8
  • Why do you need it in FORTRAN-like style? Mathematica has its own strengths. – rhermans Sep 12 '14 at 15:04
  • Explicit programming of step evolution for numerical differential solving is not really needed in Mathematica, since NDSolve is already built-in, and has options for controlling the method used. That's not to say that you can't program the solution like you would in Fortran, but if you did, you would be disappointed at the performance. The reason Mathematica exists is to make it so that you don't have to waste time explicitly writing Fortran-like loops when doing a numerical solution. – DumpsterDoofus Sep 12 '14 at 15:14
  • Fair enough to use mathematica to learn procedural programming, but you need to show what you have tried. As is we dont know where to begin. The mathematica equivalent of Fortran do is Do .. – george2079 Sep 12 '14 at 15:15
  • Procedural programming is usually not the best way to go in Mathematica. I could show you how to implement the method of solution illustrated in Feynman's Lectures on Physics by using NestList. It uses position and velocities to compute the acceleration and velocities and position at subsequent instants of time. Interested? – Peltio Sep 12 '14 at 15:29
  • If the goal is to do the time-stepping yourself, then I think it's a duplicate of RK4 Gravity Simulator. – Jens Sep 12 '14 at 16:44

2 Answers2

2

Let me make a couple of points:

  • Convert your equation into a proper differential equation, i.e. r''[t] == -GM/Norm[r[t]]^3 r[t]

  • Even better, write it in Cartesian coordinates. Remember that Norm[r[t]] equals Sqrt[ x[t]^2 + y[t]^2]. Also remember, that the orbit is always in a plane, so you can chose your coordinates accordingly and drop the equation for z[t]

    deq = { 
          x''[t] == -GM x[t]/(x[t]^2 + y[t]^2)^(3/2) ,
          y''[t] == -GM y[t]/(x[t]^2 + y[t]^2)^(3/2) 
      };

  • Use proper units. For the Earth orbiting the Sun, it is useful to choose 1 AU as the unit of length (this way the radius of the orbit is 1, ignoring eccentricity, of course) and 1 year as the unit of time

  • If you use those units, you can easily figure out that with an initial radius of 1 (e.g. given by x[0]==1, y[0]==0, the initial velocity must be 2[\Pi] (e.g. x'[0]==0, y'[0]==2[\Pi] - simply divide the length of the orbit by the time it tales to complete it.

    deqIC = {x[0] == 1,
         y[0] == 0, 
        x'[0] == 0 , 
        y'[0] == 2 \[Pi]};

  • By pretty much the same argument, GM = (2[\Pi])^2

Now you can simply dump the differential equation into NDSolve and let Mathematica do the rest:

s = Reap@NDSolve[ Join[deq, deqIC], {x, y}, {t, 0, 1},
     MaxSteps -> 100000,
    InterpolationOrder -> Automatic,
    Method -> "ExplicitRungeKutta",
    StepMonitor :> Sow[ {x[t], y[t]}]
];

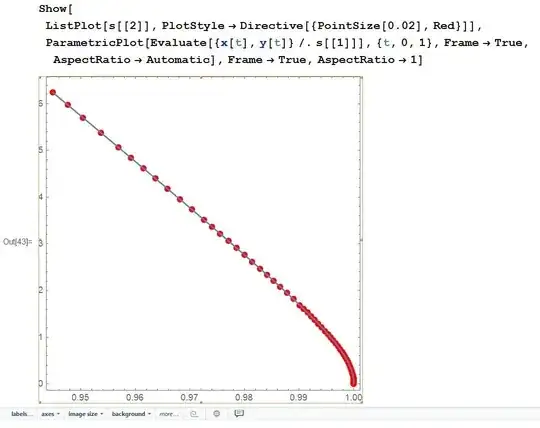
Show[ ListPlot[s[[2]],   PlotStyle -> Directive[{PointSize[0.02], Red}]], 
 ParametricPlot[Evaluate[{x[t], y[t]} /. s[[1]]], {t, 0, 1}, 
  Frame -> True, AspectRatio -> Automatic],
 Frame -> True, AspectRatio -> Automatic]

The Sow/Reap stuff is only showing off - you can get the actual points at which Mathematica evaluates your differential equation.

As far as FORTRAN goes - if this isn't a homework where you have to use FORTRAN, forget about it. There is no advantage in using FORTRAN code and branch out to Mathematica just for the plotting.

george2079
  • 38,913
  • 1
  • 43
  • 110
Oliver Jennrich
  • 1,194
  • 5
  • 12
  • Unfortunately, this is a homework in which fortran like code is required. Using mathematica is purely for the plotting capabilities. Thanks for your help though! – Karl Sep 12 '14 at 20:55
1

This is not an answer, but it can not fit into a comment.

Above Show[ListPlot[...]..[ produces following graph for the earth's orbit around sun. Is this the correct orbit?

enter image description here

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
Max Jasper
  • 153
  • 5
  • Apparently the initial velocity is too high and the Earth is flying off on a hyperbola. –  Sep 12 '14 at 18:47
  • 1
    It can be fitted into the comment. You can use hyperlinks: [image](http://i.stack.imgur.com/sX42C.jpg) which will be converted to image. – ybeltukov Sep 12 '14 at 19:21