5

I would like to accurately distort this plot of $\sin(x^{1/2})$ (and others like it) so that the wavelengths are evened out (ie - "inverse-square root" it).

enter image description here

I should like to do the same to "de-log" plots too.

I have no idea where to start though.

martin
  • 8,678
  • 4
  • 23
  • 70
  • Well, if $f(x) = \sin(x^2)$, you could just plot $f(\sqrt x)$ instead? Pretty sure what you have there's not a plot of $\sin(x^2)$ though. –  Sep 14 '14 at 01:34
  • Yes, sin(x^2) should be zero at the origin. – Shredderroy Sep 14 '14 at 01:54
  • Sorry - corrected. I would like to distort images with this proportion - the plot was just an eg – martin Sep 14 '14 at 02:27
  • 1
    There are lots of ways to do this, but you probably need to be more specific. The words "accurate" and "distort" seem to be at odds. One way would be Sin[Sqrt[x]] /. x -> x^2/1000. Another, if you want to "morph" the graphs would be (1 - t) Sqrt[x] + t x / Sqrt[1000], for t running from 0 to 1. That's assuming x ranges from 0 to 1000. – Michael E2 Sep 14 '14 at 02:45
  • It is images really that I would like to distort - including the axes etc. I shall probably have to reword it in the morning! – martin Sep 14 '14 at 02:55

3 Answers3

6
plt1 = Plot[Sin[Sqrt[x]], {x, 0, 1000}, ImageSize -> 400];

ticks = Ticks /. AbsoluteOptions[plt1, Ticks];
ticks = MapAt[#^(1/2) &, ticks, {{1, All, 1}}];
plotrange = PlotRange[plt1];
plotrange = MapAt[#^(1/2) &, plotrange, {1}]; 

plt2 = Graphics[plt1[[1]] /. Line[x_] :> Line[{#[[1]]^(1/2), #[[2]]} & /@ x], 
                PlotRange -> plotrange, Ticks -> ticks, plt1[[2]]];
Row[{plt1, plt2}]

enter image description here

Update: The approach above works without issue in Version 9.0.1.0 (Windows 8 64bit). Unfortunately it does not work in Version 10 because AbsoluteOptions stopped working as expected in Version 10. A work-around until the AbsoluteOptions glitch is fixed (hopefully in Version 10.0.1.0) is to specify the ticks directly:

ticksb = {{#^(1/2),#}&/@FindDivisions[{0,1000},{5}][[1]],Automatic};
plt2b = Graphics[plt1[[1]] /. Line[x_] :> Line[{#[[1]]^(1/2), #[[2]]} & /@ x], 
            PlotRange -> plotrange, Ticks -> ticksb, plt1[[2]]];
Row[{plt1, plt2b}]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896
  • brilliant! Thank you! – martin Sep 14 '14 at 08:31
  • I am getting the following errors ... any ideas? Axes::axes: {{False,False},{False,False}} is not a valid axis specification. >>`` Axes::axes: {{False,False},{False,False}} is not a valid axis specification. >>`` Ticks::ticks: {Automatic,Automatic} is not a valid tick specification. >>`` Ticks::ticks: {Automatic,Automatic} is not a valid tick specification. >>`` Axes::axes: {{False,False},{False,False}} is not a valid axis specification. >>`` General::stop: Further output of Axes::axes will be suppressed during this calculation. >> – martin Sep 14 '14 at 08:35
  • do I need to load a package? – martin Sep 14 '14 at 09:43
  • @martin, this works without issue with in 9.0.1.0 (Windows 8 64bit). Just confirmed that it does not work in Version 10 because AbsoluteOptions stopped working es expected in Version 10. I will try to find a workaround to handle the ticks. (The rest of the code works if you you comment out the parts involving ticks) – kglr Sep 14 '14 at 10:05
  • Great, thanks :) – martin Sep 14 '14 at 10:26
  • Works perfectly - thank you! – martin Sep 14 '14 at 10:48
  • it doesn't seem to like it if I replace #^(1/2) with Log[#]. Am I missing something? – martin Sep 14 '14 at 11:50
  • 1
    @Martin, I think Log[0] (Indeterminate) in ticksb and plotrange is the source of the problem. You can either (1) change the range {0,1000} to {1,1000} or (2) use ticksb /. Indeterminate->0 instead of ticksb and similarly for plotrange. – kglr Sep 14 '14 at 14:09
  • Great, thanks :) – martin Sep 14 '14 at 14:12
3

Here is an attempt to do this using the internal options used by LogPlot etc. It has the advantage of correctly working with the adaptive sampling of Plot to produce a better result with extreme scaling.

SetAttributes[scaledPlot, HoldRest]

scaledPlot[scfn_, exp_, {s_, r1_, r2_}, arg___] :=
 With[{inv = InverseFunction[scfn]},
   Plot[exp, {s, scfn[r1], scfn[r2]}, arg, 
     Method -> {"MappingFunctions" -> {{#1, #2} &, {#1, #2} &}, 
                "DomainMappingFunctions" -> {inv}},
     Ticks -> {Charting`ScaledTicks[{scfn, inv}], Automatic}
   ]
 ]

Examples:

scaledPlot[Sqrt, Sin[x^(1/2)], {x, 0, 1000}]

enter image description here

scaledPlot[#^(1/4) &, Sin[x^(1/4)], {x, 0, 2*^6}]

enter image description here

Compare the second result with the same plot using kguler's method and the value of adaptive sampling becomes apparent:

plt1 = Plot[Sin[x^(1/4)], {x, 0, 2*^6}, ImageSize -> 400];
ticksb = {{#^(1/4), #} & /@ FindDivisions[{0, 2*^6}, {5}][[1]], Automatic};
plt2b = Graphics[plt1[[1]] /. Line[x_] :> Line[{#[[1]]^(1/4), #[[2]]} & /@ x], 
  PlotRange -> plotrange, Ticks -> ticksb, plt1[[2]]]

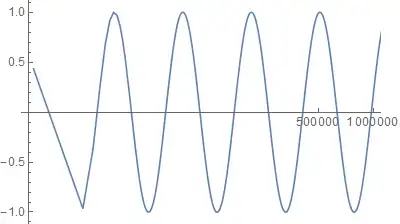
enter image description here

The more extreme the scaling the worse this problem will become, and adding PlotPoints will not overcome it. (e.g. try x^(1/9))

Note: Sometimes the tick marks disappear, e.g. with #^(1/3) &. This seems like a problem with Charting`ScaledTicks but one can always specify a list of ticks manually if necessary.

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • this is really great - should have waited before accepting :/ Thank you! – martin Sep 14 '14 at 14:09
  • Is it possible to use this with ListLinePlot? – martin Sep 14 '14 at 14:13
  • 1
    @martin (1) Thanks. (2) Yes, I recommend waiting a bit longer before Accepting an answer. However, if you feel so inclined you can change (or remove) your Accept at any time. (3) I don't believe these Method options apply to ListLinePlot, but since you wouldn't get adaptive sampling there anyway a manual scaling approach seems reasonable. – Mr.Wizard Sep 14 '14 at 14:25
  • Thanks for the advice - really great answer - I feel a bit mean unaccepting an answer though ... :/ – martin Sep 14 '14 at 14:35
0

Based on your last comment and if I understand it correctly, you want to work with the image itself. If so, maybe something like this would help.

img = Plot[Sin[Sqrt[x]], {x, 0, 1000}];

 ImageTransformation[img, {#[[1]]^2, #[[2]]} &]
Basheer Algohi
  • 19,917
  • 1
  • 31
  • 78