I think the problem is not with Mathematica or your understanding of it but with the mathematics of that equation and it isn't even a singularity which would show for Epsilon->0. The problem is that your equations have a problem when the derivative w'[x] becomes 0, and that does happen already for much higher values of Epsilon (I have renamed that to eps in the following):
data = {Q -> 1, R -> 1}
eqs[eps_] := {
w''[x] w'[x] + 3 Q w[x]^2 - 2 R w[x] w'[x] == 0,
w[eps] == 1, w[1] == 0.8
} /. data;
eps = 0.75567;
s = NDSolveValue[eqs[eps], w, {x, eps, 1}];
Plot[{s[x], s'[x]}, {x, eps, 1},Frame->True]
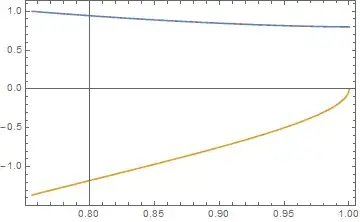
note that the critical point isn't at the lowest x-values but at the endpoint x=1, for roughly the given eps-value the derivative effectively gets zero and that seems to be the source of your problem. Solving the differential equations for w''[x] is another way to see the source of the problem. Here is an Animation that illustrates what happens when you decrease the x value where the initial condition is set:
Animate[
s = NDSolveValue[eqs[eps], w, {x, eps, 1}];
Plot[{s[x], s'[x]}, {x, eps, 1}, Frame -> True,
PlotRange -> {{0.7, 1}, {-4, 2}}],
{eps, 0.75567, 0.99}, AnimationDirection -> Backward
]
EDIT
Actually you will find that older versions of Mathematica won't return a result even for values for eps larger than the one I have given. This does indicate that the equations are problematic and as has been mentioned by xzczd that is of course an indication that the results that Version 10 gives might also not be trusted blindly. If you know that there are sigularities in a differentital equations any way to solve it numerically needs some extra effort to justify that the result is correct.
EDIT
In a comment xzczd has mentioned that the original code didn't return the same result reliably when playing around with eps. I have also seen that behavior and updated the code in a way that I think will not show that problem. It is a good example why it is always a good idea to make dependendcies of your equations/formulae/functions explicit...

Block[{Epsilon = $MachineEpsilon}...– Michael E2 Sep 14 '14 at 23:47w'[1]==0. Try this code:s = ParametricNDSolveValue[{w''[x] w'[x] + 3 w[x]^2 - 2 w[x] w'[x] == 0, w[1] == 0.8, w'[1] == a}, w, {x, 0, 1}, a]; Plot[s[a][0], {a, -1, 1}]. – xzczd Sep 16 '14 at 03:50