8

What possibilities are there for time-frequency analysis in Mathematica beyond wavelet decomposition? I could not even find a simple STFT.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Emre
  • 1,720
  • 2
  • 13
  • 21
  • 2
    See this question for a spectrogram. – rm -rf May 23 '12 at 23:49
  • 1
    See: Fractional Fourier transform, http://mathworld.wolfram.com/FractionalFourierTransform.html it has a downloadable notebook – Jagra May 23 '12 at 23:50
  • 2
    you can use Wigner distribution function ... see demos... http://demonstrations.wolfram.com/WignerFunctionOfHarmonicOscillator/ http://demonstrations.wolfram.com/WignerFunctionOfACanonicalEnsembleOfHarmonicOscillatorsAtAGi/ http://demonstrations.wolfram.com/WignerFunctionOfTwoDimensionalIsotropicHarmonicOscillator/ – s.s.o May 24 '12 at 00:03

2 Answers2

12

The links provide you with everything you need I think. The goal of this answer is to show you that even though it's not built in, a discrete STFT is quite easy and short to code.

This would take the DFT of the data set partitioned into chunks of length 2^13, with half a window overlap, and a rectangular window

STFT[r_]:= Fourier /@ Partition[r, 2^13, 2^12];

That's the end of it.

Of course it would take a little more to make a function with options such as Overlap, some option to automatically drop the negative frequencies for real inputs, window type, DFT length... But all of them are immediate to implement. I just saw the very neat @RM's implementation. You should go check it out.

Legacy code from before having seen the link with enough attention:

Options[STFT] = {"Overlap" -> 0.5, 
   "DropNegativeFrequenciesForRealInputs" -> True, 
   "Window" -> ConstantArray[1, 2^10], "DFTLength" -> 2^10};

STFT[r_, OptionsPattern[]] :=
  With[{wlen = OptionValue["DFTLength"]},
   With[{w = PadRight[OptionValue["Window"], wlen], 
     wstep = Round[wlen (1 - OptionValue["Overlap"])]},
    If[r \[Element] Reals, 
       Take[#, All, Round[Last@Dimensions@#]/2], #] &[
     Fourier /@ (w # &) /@ Partition[r, wlen, wstep]]]
   ];
Community
  • 1
Rojo
  • 42,601
  • 7
  • 96
  • 188
5

we can do a STFT of Sin[Pi*t^4]

f[t_] := Sin[Pi*t^4];
fs=1000.(*Hz*);
data = Table[f[t], {t, 0, 5, 1/fs}];
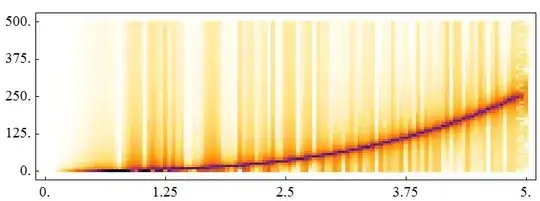
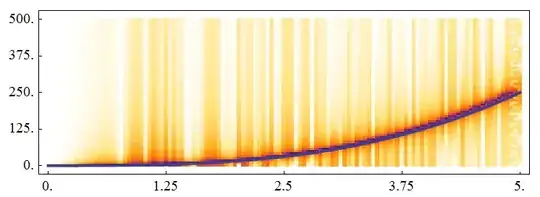
Spectrogram[data, SampleRate -> fs]

enter image description here

the instantaneous frequency of f[t] is $$\frac{f'(t)}{2 \pi }$$ So the ideal instantaneous frequency is:

Plot[Evaluate[D[Pi*t^4, t]/(2 Pi)], {t, 0, 5}]

enter image description here

Ok,Combine the two image: enter image description here

Well done.Mathematica gives a fine result.

partida
  • 6,816
  • 22
  • 48