drawing core-shell structure

Question

I am pretty new in Mathematica drawing. I am trying to draw a core-shell structure, it means a core sphere with a shell sphere, like this

enter image description here

It can be in 2D or preferentially in 3D. Does someone can help me?

I tried the commands ParametricPlot3D[] and Sphere[], but they do not work. I want to do just a draw (core-shell structure) like in the link. — Vagner Zeizer Carvalho Paes, Sep 15 '14 at 17:50
Somewhat close: http://mathematica.stackexchange.com/questions/47713/add-coordinate-axes-to-a-3d-plot-of-concentric-spheres — Michael E2, Sep 15 '14 at 18:33

score 6 · Accepted Answer · answered Sep 15 '14 at 17:58

6

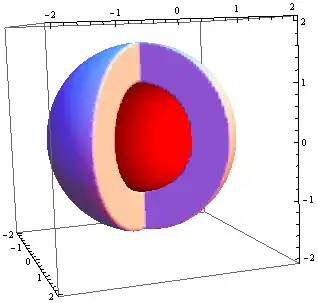
Show[RegionPlot3D[1 <= x^2 + y^2 + z^2 <= 3 && (y >= x Sin[Pi/2] || y < -x Sin[Pi/2]),   
                  {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Mesh -> None, PlotPoints -> 100], 
     Graphics3D[{Red, Sphere[{0, 0, 0}, 1]}]]

Mathematica graphics

answered Sep 15 '14 at 17:58

Dr. belisarius

115,881
13
203
453

1

To avoid the blurry edges in the region plot, see this nice method. – Sep 15 '14 at 19:53
@RahulNarain Thanks! That's very nice. – Dr. belisarius Sep 15 '14 at 19:59

eldo · Answer 2 · 2014-09-15T20:03:41.650

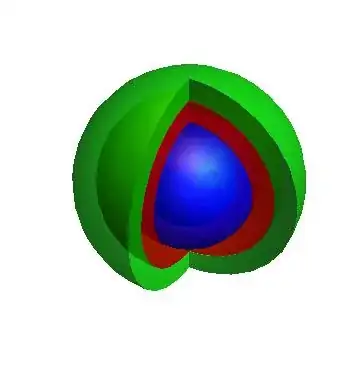
SetOptions[{SphericalPlot3D, ParametricPlot3D}, Mesh -> None];

fun = {r {0, -Sin[t], Cos[t]}, r {Sin[t], 0, Cos[t]}};

p1 = SphericalPlot3D[{2, 2.5}, {u, 0, Pi}, {v, 0, 1.5 Pi}, 
   PlotStyle -> 
    Directive[Green, Opacity[0.7], Specularity[White, 20]]];

p2 = ParametricPlot3D[fun, {r, 2, 2.5}, {t, 0, Pi}, 
   PlotStyle -> 
    Directive[Green, Opacity[0.7], Specularity[White, 20]]];

p3 = SphericalPlot3D[{1.5, 1.99}, {u, 0, Pi}, {v, 0, 1.5 Pi}, 
   PlotStyle -> Directive[Red, Opacity[0.7], Specularity[White, 20]]];

p4 = ParametricPlot3D[fun, {r, 1.5, 1.99}, {t, 0, Pi}, 
   PlotStyle -> Directive[Red, Opacity[0.7], Specularity[White, 20]]];

p5 = SphericalPlot3D[{1, 1.48}, {u, 0, Pi}, {v, 0, 2 Pi}, 
   PlotStyle -> Directive[Blue, Opacity[0.7], Specularity[White, 20]]];

Show[p1, p2, p3, p4, p5, PlotRange -> All, Axes -> False, 
 Boxed -> False]

enter image description here

Show[p1, p2, p3, p4, p5, PlotRange -> All, ViewPoint -> Front]

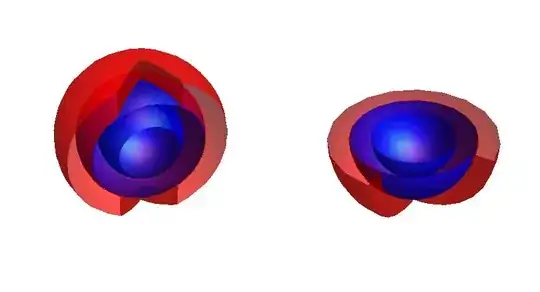
enter image description here

 Grid[{{

   Show[p3, p4, p5, ClipPlanes -> {{-1, 1, 0, 1}},
    Axes -> False, Boxed -> False, ImageSize -> 400],

   Show[p3, p4, p5, ClipPlanes -> {{0, 0, -1, 0}},
    Axes -> False, Boxed -> False, ImageSize -> 400]}}]

enter image description here

thank you a lot! that is what I was looking for! – Vagner Zeizer Carvalho Paes Sep 15 '14 at 22:05 — Vagner Zeizer Carvalho Paes, Sep 15 '14 at 22:05

score 3 · Answer 3 · answered Sep 15 '14 at 19:10

 p = N@Table[  { Cos[x], 0, Sin[x]}, {x, Pi/2, -Pi/2, -Pi/200}];
 Show[ 
      {
     SphericalPlot3D[ 1 , {t, 0, Pi}, {phi, 0, 3 Pi/2}, Axes -> False, Mesh -> False],
     Graphics3D@{{Red, Sphere[{0, 0, 0}, 1/2]},
                 Polygon[ p],
                 Polygon@(RotationTransform[-Pi/2, {0, 0, 1}]@p)
         }} , Boxed -> False ]

enter image description here

Narasimham · Answer 4 · 2014-09-15T20:05:56.617

This is adapted from 3D solid modeling thick cylindrical shell done before (also ref. Mma site). Here it generates volume between two concentric spherical shells separately in three modes, for any desired choice. Hope it may be suitable.

 1. sweeps along parallels... t
 2. sweeps along meridians ...v ,or,
 3. dilates along shell normal, sphere expands or shrinks...a

Thick Spherical Shell & Core

ThickShell[a_, t_, v_] = a {Cos[t] Cos[v], Sin[t], Cos[t] Sin[v]}; (* GLNarasimham SolidModelingThickShell.nb *) Manipulate[ Row[{ParametricPlot3D[{Cos[t] Cos[u], Sin[u], Cos[u] Sin[t]}, {t, 0, 2 Pi}, {u, -1.5, 1.5}, ImageSize -> 300, ViewPoint -> {3, 1, 2}], ParametricPlot3D[ThickShell[a, t, v], {v, 0, 2 Pi}, {a, 1, 1.6}, Mesh -> {18, 4}, ImageSize -> 300, PlotRange -> {{-1.8, 1.8}, {-2, 2}, {-1.8, 1.8}}, ViewPoint -> {3, 1, 2}], ParametricPlot3D[ThickShell[a, t, v], {t, 0, 2 Pi}, {a, 1, 1.6}, Mesh -> {18, 4}, ImageSize -> 300, PlotRange -> {{-1.8, 1.8}, {-2, 2}, {-1.8, 1.8}}, ViewPoint -> {3, 1, 2}], ParametricPlot3D[ThickShell[a, t, v], {t, 0, 2 Pi}, {v, 0, 2 Pi}, Mesh -> {18, 18}, ImageSize -> 300, PlotRange -> {{-1.8, 1.8}, {-2, 2}, {-1.8, 1.8}}, ViewPoint -> {3, 1, 2}]}], {t, 0, 2 Pi, Pi/5}, {v, 0, 2 Pi, Pi/10}, {a, 1, 1.6, .05}]

drawing core-shell structure

4 Answers4

Linked