A question regarding "DiscretizeGraphics"

Question

I want to find the volume of a torus

torus =
 RevolutionPlot3D[{2 + Cos[t], Sin[t]}, {t, 0, 2 Pi}]

enter image description here

dtorus =
 DiscretizeGraphics[Cases[Normal @ torus, _GraphicsGroup, -1][[1]]]

enter image description here

The Documentation for RegionMeasure states:

"RegionMeasure is also known as count (0D), length (1D), area (2D), volume (3D)..."

{Area @ dtorus, RegionMeasure @ dtorus, Volume @ dtorus}

{78.6557, 78.6557, 0}

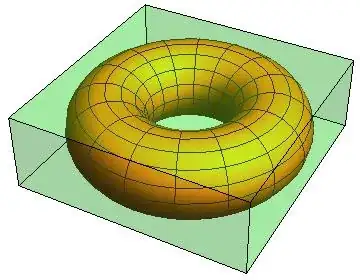
Next, I want to find the volume of the torus' bounding cuboid

bounds = RegionBounds[dtorus]

{{-3., 3.}, {-3., 3.}, {-1., 1.}}

cuboid =
  Graphics3D[{Green, Opacity @ 0.2, Cuboid @@ Transpose[bounds]}];

Show[torus, cuboid, Boxed -> False, Axes -> False]

enter image description here

Now find the volume of the cuboid

dcuboid =
 DiscretizeGraphics @ cuboid

enter image description here

{Area @ dcuboid, RegionMeasure @ dcuboid, Volume @ dcuboid}

{Infinity, 72., 72.}

Questions

How can it be that the Volume of the bounding cuboid, 72, is lower than the "Volume" of the torus, 78 .6557?

What do I overlook here?

What other options do I have to find the volume of my torus?

But isn't the volume of your torus 0? {Area @ dtorus, RegionMeasure @ dtorus, Volume @ dtorus}->{78.6557, 78.6557, 0}. As I understand, RevolutionPlot3D plots a surface. A surface itself has 0 volume, for instance, a sphere. — Grzegorz Rut, Sep 17 '14 at 12:39
@GregoryRut A sphere has volume 4/3 Pi * radius^3, hasn't it? — eldo, Sep 17 '14 at 12:48
No, it's somehing different. A ball has a volume. You could define an interior volume of a sphere. — Grzegorz Rut, Sep 17 '14 at 12:49
If you do RegionDimension[dtorus], you'll see why. In this case RegionMeasure is giving you the surface area of the torus since you have a 2D region. — RunnyKine, Sep 17 '14 at 14:43
@RunnyKine Kind of pity that you didn't write your comment as an answer. My dtorus transformed a gentle three-dimensioal subject into dumb two-dimensional polygon-objects. — eldo, Sep 17 '14 at 19:11
I guess I didn't have time to expand on it at the time. Maybe I'll do that and show more examples later. — RunnyKine, Sep 17 '14 at 19:13
If you do RevolutionPlot3D[{2 + Cos[t], Sin[t]}, {t, Pi/2, 2 Pi}] it should be clear that in general one cannot expect a RevolutionPlot3D to describe a volumetric object. http://i.stack.imgur.com/SJAhk.png — , Sep 17 '14 at 20:20
@RahulNarain, the truth is, DiscretizeGraphics will almost always give a surface discretization regardless of how the graphics was generated, which will result in a 2D region in general. — RunnyKine, Sep 17 '14 at 20:31

Grzegorz Rut · Accepted Answer · 2014-09-17T17:44:00.697

As I have mentioned in my comment, in order to define a torus with a volume, you need an inequality. Just like you would define the interior of a sphere: $x^2+y^2+z^2<R^2$. The interior of the torus is defined by an inequality $\left(R - \sqrt{x^2 + y^2}\right)^2 + z^2 < r^2 $, where R and r are the major and minor radii, respectively.

tor[R_, r_, x_, y_, z_] := (R - Sqrt[x^2 + y^2])^2 + z^2 < r^2

Volume@DiscretizeRegion[
  ImplicitRegion[
   tor[2, 1, x, y, z], {x, y, z}], {{-3, 3}, {-3, 3}, {-3, 3}}]
(*38.30219*)

The formula for interior volume of a torus reads $ V = 2 \pi^2 R r^2.$ In our case the volume would be roughly $V\approx $39.5.

It seems that Volume could be applied for 'derived regions' (like tor, for instance) yet it seems that it works only for selected types of areas.

Why do you use 6 instead of 2 Pi ? 2 Piwould give 305.657 — eldo, Sep 17 '14 at 12:59
There was an error with def. of tor function (R^2 instead of R). It's fixed now. The range of variables has been modified as well. — Grzegorz Rut, Sep 17 '14 at 13:18

score 9 · Answer 2 · answered Sep 17 '14 at 19:50

I'm not 100% sure on this, but I think you can construct a torus as a Cartesian product of a disk and a circle. Unfortunately you can't visualise it because the embedding dimension is 4, but the volume seems to come out correct:

Volume @ RegionProduct[Disk[{0, 0}, 1], Circle[{0, 0}, 2]]

(*  4 π^2  *)

or with symbolic radii:

Volume @ RegionProduct[Disk[{0, 0}, r], Circle[{0, 0}, R]]

(* 2 π^2 r^2 R *)

score 2 · Answer 3 · answered Feb 25 '24 at 02:35

Now we can set

Mesh -> None, Method -> {"BoundaryOffset" -> False}

Thanks @MichaelE2

https://mathematica.stackexchange.com/a/92557/72111

https://mathematica.stackexchange.com/a/226367/72111

torus2 = 
  RevolutionPlot3D[{2 + Cos[t], Sin[t]}, {t, 0, 2  Pi}, Mesh -> None, 
   Method -> {"BoundaryOffset" -> False}, PlotPoints -> 60];
reg = torus2 // BoundaryDiscretizeGraphics
FindMeshDefects[reg]
Volume[reg]

39.3297

A question regarding "DiscretizeGraphics"

3 Answers3