8

I'm trying to find the inverse of a function: 

(30*x^2 (1 - x)^2) (* where 0<x<1 *)

I tried all the following options:

1.

InverseFunction[ConditionalExpression[30*#1^2 (1 - #1)^2, 0 < #1 < 1] &]

2.

f = Function[30*#^2 (1 - #)^2] &

g = InverseFunction[f]

3.

g[x_] = 30*x^2 (1 - x)^2

sol = Solve[y == x^2 &&  0 < x < 1, x]

D[x /. sol[[1]], y]

Thank you so much in advance!

kglr
  • 394,356
  • 18
  • 477
  • 896
user19754
  • 193
  • 1
  • 6

5 Answers5

11

Solve also works

Solve[y == 30 x^2 (1 - x)^2 && 0 < x < 1, x, Reals]

{{x -> ConditionalExpression[Root[-y + 30 #1^2 - 60 #1^3 + 30 #1^4 &, 2], 0 < y < 15/8]}, 
 {x -> ConditionalExpression[Root[-y + 30 #1^2 - 60 #1^3 + 30 #1^4 &, 3], 0 < y < 15/8]}}

Use ToRadicals to get it in a nice looking form.

Netsie
  • 126
  • 4
8

Your second approach is nearly correct. Modify it like so.

f = 30*#^2 (1 - #)^2 &;
g = InverseFunction[f]

1/30 (15 - Sqrt[15] Sqrt[15 - 2 Sqrt[30] Sqrt[#1]]) &

Plot[f[g[x]], {x, 0, 1}]

plot

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
  • 1
    Hm... I overlooked that mistake. +1 – Mr.Wizard Sep 20 '14 at 13:11
  • this gives an error "InverseFunction::ifun: Inverse functions are being used. Values may be lost for multivalued inverses. " – user19754 Sep 20 '14 at 13:14
  • 1
    @user19754 Right. See my answer for a different treatment. – Mr.Wizard Sep 20 '14 at 13:17
  • @user19754. It's not an error message. It's a warning. In the domain {0, 1}, the g is fine. In the domain x < 0, it is not valid. You can turn it off with Quiet. – m_goldberg Sep 20 '14 at 13:22
  • @m_goldberg Are you saying that one of the branches I show is invalid or do you mean something else? – Mr.Wizard Sep 20 '14 at 13:23
  • 2
    @Mr.Wizard. In the domain {0,1}, specified by the OP, either brach will work. The way the question is posed, makes me think the OP would be satisfied by any functional form that works in his domain, and and is not interested in the complete set. – m_goldberg Sep 20 '14 at 13:36
6

Reduce appears to provide useful information:

Reduce[{(30*x^2 (1 - x)^2) == y, 0 < x < 1}, x, Reals]

(0 < y < 15/8 && (x == Root[-y + 30 #1^2 - 60 #1^3 + 30 #1^4 &, 2] || 
     x == Root[-y + 30 #1^2 - 60 #1^3 + 30 #1^4 &, 3])) || (y == 15/8 && x == 1/2)

ToRadicals can be used to put this into a more familiar form.

% // ToRadicals

(0 < y < 15/8 && (x == 1/2 (1 + Sqrt[15 - 2 Sqrt[30] Sqrt[y]]/Sqrt[15]) || 
     x == 1/2 (1 - Sqrt[15 + 2 Sqrt[30] Sqrt[y]]/Sqrt[15]))) || (y == 15/8 && x == 1/2)

Branches:

Plot[
 {1/2 (1 + Sqrt[15 - 2 Sqrt[30] Sqrt[y]]/Sqrt[15]), 
  1/2 (1 - Sqrt[15 + 2 Sqrt[30] Sqrt[y]]/Sqrt[15])},
 {y, 0, 15/8}
]

enter image description here

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
6

A good comprehensive answer should explain why InverseFunction "didn't work", however there's been no explanation so far. A unique inverse function can be found in a region if there its jacobian is nondegenerate, i.e. its determinant doesn't vanish (Inverse function theorem) . For one - variable function it means that the derivative doesn't vanish.

Reduce[ D[ 30 #1^2 (1 - #1)^2 &[x], x] != 0, x, Reals]

x < 0 || 0 < x < 1/2 || 1/2 < x < 1 || x > 1

Now taking any of the specified ranges InverseFunction works expectedly:

InverseFunction[ ConditionalExpression[30*#1^2 (1 - #1)^2, 0 < #1 < 1/2] &][y]

ConditionalExpression[Root[-y + 30 #1^2 - 60 #1^3 + 30 #1^4 &, 2], 0 < y < 15/8] 

InverseFunction[ ConditionalExpression[30*#1^2 (1 - #1)^2, 1/2 < #1 < 1] &][y]

ConditionalExpression[Root[-y + 30 #1^2 - 60 #1^3 + 30 #1^4 &, 3], 0 < y < 15/8]

so depending on the region inverse function might be any of Root[-y + 30 #1^2 - 60 #1^3 + 30 #1^4 &, k] for $k=1\ldots4$.

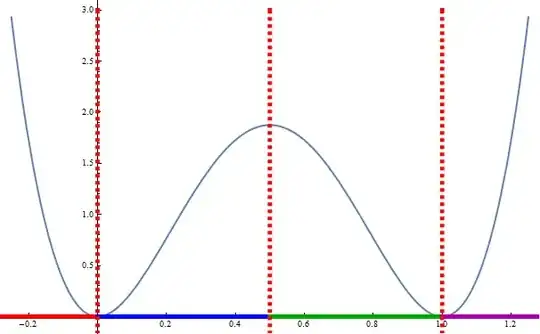
Invertibility of the given function is restrected to appropriate regions, this can be easily seen from the following plot

Plot[ 30 #1^2 (1 - #1)^2 &[x], {x, -1/4, 5/4}, PlotStyle -> Thick,
      Epilog -> {Red, Thickness[0.008], Line[{{-1/2, 0}, {0, 0}}], 
                 Blue, Line[{{0, 0}, {1/2, 0}}], 
                 Darker @ Green, Line[{{1/2, 0}, {1, 0}}], 
                 Darker @ Magenta, Line[{{1, 0}, {3/2, 0}}], 
                 Red, Dashed, Line[{{{0, 3}, {0, -1}}, {{1/2, 3}, {1/2, -1}}, 
                                   {{1, 3}, {1, -1}}}]}]

enter image description here

Artes
  • 57,212
  • 12
  • 157
  • 245
  • Artes, this is a great explanation. How do we deal with functions such as the one given in this question where there are multiple monotone regions? For example y=x^2 is monotone on $(-\infty,0)$ and $(0, \infty)$ . Is it possible for mathematica to recognize that and give two answers like -sqrt(y) for the first region and and sqrt(y) for the second? – user19754 Sep 21 '14 at 14:49
  • 1
    @user19754 Great? No upvotes so far... Reduce[y == x^2, x, Reals] yields y >= 0 && (x == -Sqrt[y] || x == Sqrt[y]). Perhaps also FunctionDomain[InverseFunction[#^2 &][x], x] could be useful however this should be more a bit precise question. – Artes Sep 21 '14 at 15:19
  • Artes, Reduce[y == x^2 && x > -1 && x < 1, x, Reals] works, giving (0 < y < 1 && (x == -Sqrt[y] || x == Sqrt[y]), but it does not give us the information that for -Sqrt[y] x must be from -1 to 0 and for the other one, from 0 to 1. I'm sorry if my question is confusing – user19754 Sep 21 '14 at 16:06
1
purify[f_, x_] := Function @@ {f /. x -> #}

fun = 30*x^2 (1 - x)^2;

inv = InverseFunction[purify[fun, x]][x] // Quiet

enter image description here

LogPlot[{fun, inv}, {x, 0, 1}, PlotTheme -> "Detailed"]

enter image description here

eldo
  • 67,911
  • 5
  • 60
  • 168