An alternative approach is to use Mesh and MeshFunctions as follows:
ClearAll[f, g];
f = 2/(1 + 20 x^2);
g = 1/(1 + 20 x^2)^(1/2);
Plot[{f, g}, {x, 0, 3},
MeshFunctions -> {(f - g) /. x -> # &}, Mesh -> {{0}},
MeshStyle -> Directive[Red, PointSize[Large]],
AxesLabel -> {"x", "y"}, LabelStyle -> (FontSize -> 16),
GridLines -> Automatic, PlotRange -> {0, 3}]

ClearAll[f2, g2, x];
f2 = 3/(3 + 20 (Sin@x - 1/2)^2);
g2 = 1/(1 + 5 (Sin[x] - 3/10)^2)^(1/2);
Plot[{f2, g2}, {x, 0, 3}, MeshFunctions -> {(f2 - g2) /. x -> # &},
Mesh -> {{0}}, MeshStyle -> Directive[Red, PointSize[Large]],
AxesLabel -> {"x", "y"}, LabelStyle -> (FontSize -> 16),
GridLines -> Automatic, PlotRange -> {0, 3/2}]

You can also find the mesh points by using Solve instead of using MeshFunctions:
mesh = Last @@@ N[Solve[{f2 == g2, 0 <= x <= 3}, x, Reals] ]
(* {2.7032,0.438392,2.29184,0.849753} *)
Plot[{f2, g2}, {x, 0, 3}, Mesh -> {mesh},
MeshStyle -> Directive[Red, PointSize[Large]],
AxesLabel -> {"x", "y"}, LabelStyle -> (FontSize -> 16),
GridLines -> Automatic, PlotRange -> {0, 3/2}]
(* same picture *)
Update: You can also use the function Graphics`Mesh`FindIntersections to find the intersections in a graphics object:
plot = Plot[{f2, g2}, {x, 0, 3}, AxesLabel -> {"x", "y"},
LabelStyle -> (FontSize -> 16), GridLines -> Automatic,
PlotRange -> {0, 3/2}];
Graphics`Mesh`MeshInit[];
Show[plot, Graphics[{Red, PointSize[Large], Point @ FindIntersections[plot]}]]




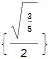


Solveinstead.Solve[2/(1 + 20 x^2) == 1/(1 + 20 x^2)^(1/2), x, Reals]– RunnyKine Sep 20 '14 at 17:27GraphIntersectiondeals with intersections of graphs (as in networks) and has nothing to do with intersections of plot lines. – Sjoerd C. de Vries Sep 20 '14 at 18:11