How to remove error at large time in NDSolve

Question

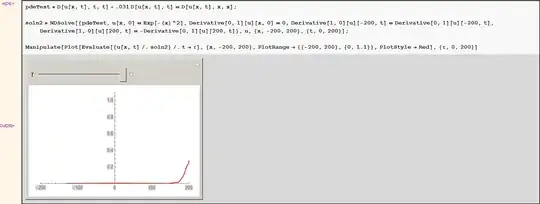
I am working with solutions of a linearly damped wave equation. In the following code I use a "transparent" boundary condition at the end, which allows waves to pass through the specified boundary so that waves do not reflect back at the boundary:

pdeTest = D[u[x, t], t, t] + .031 D[u[x, t], t] == D[u[x, t], x, x];

  soln2 = NDSolve[{pdeTest, u[x, 0] == Exp[-(x)^2],  Derivative[0, 1][u][x, 0] == 0, 
  Derivative[1, 0][u][-200, t] == Derivative[0, 1][u][-200, t], 
  Derivative[1, 0][u][200, t] == -Derivative[0, 1][u][200, t]}, 
  u, {x, -200, 200}, {t, 0, 200}];

  Manipulate[ Plot[Evaluate[{u[x, t] /. soln2} /. t -> \[Tau]], {x, -200, 200}, 
  PlotRange -> {{-200, 200}, {0, 1.1}}, PlotStyle -> Red], {\[Tau], 0, 200} ] 

This code seems to work without giving me a huge deviation using Mathematica version 8, but I have problems running it in version 9 at large times (t=200).

Intuitively, an initial wave pulse should split into two smaller wave pulses and the amplitudes of these two wave pulses should approach zero as t goes to infinity.

My code decided to blow up in Mathematica version 9. The behavior of the linearly damped wave equation is shown as expected when NDSolved and graphed in version 8. Since I am working on this project in version 9, I wanted to know how to go about fixing this problem.