I have a collection of points
{{-0.137445, -0.0103507}, {-0.0452845, 0.0343154}, {0.30498, -0.0118266}, {-0.0224633, 0.0197979},
{-0.168469, -0.0197066}, {0.0973217, 0.0478612}, {-0.0441388, 0.0360607}, {0.185982, -0.0679699},
{0.0185057, 0.0245944}, {-0.129016, 0.0581276}, {0.0759223, -0.0514376}, {0.123763, 0.0743706},
{-0.0324282, 0.0267871}, {-0.107764, -0.100215}, {0.0885256, 0.0232463}, {-0.0353817, 0.110461},
{-0.111862, -0.00308756}, {0.267131, -0.0401582}, {0.0665588, 0.0494041}, {-0.103328, 0.0535261},
{-0.107966, -0.105811}, {0.112237, 0.0221174}, {0.0250018, 0.153274}, {-0.0569079, 0.0282354},
{0.0635016, -0.142617}, {0.146519, 0.027247}, {-0.0235671, 0.0778935}, {-0.167359, 0.0314445},
{0.0472315, -0.0944644}, {0.166657, 0.0808811}, {0.0127167, 0.126777}, {-0.0896872, 0.00085879},
{0.0468778, -0.181101}, {0.0641557, 0.00642259}, {-0.00698507, 0.172202}, {-0.112879, 0.0671148},
{-0.00809596, -0.12273}, {0.211062, 0.0186191}, {0.0619741, 0.117436}, {-0.0725547, 0.0468807},
{-0.129253, -0.139777}, {0.124918, -0.0620453}, {0.0761669, 0.129845}, {-0.0510648, 0.1879},
{-0.063928, -0.0156006}, {0.133047, -0.178149}, {0.140128, 0.0330165}, {0.00229768, 0.129346},
{-0.122887, 0.0639973}, {-0.079265, -0.156894}}
that look like this
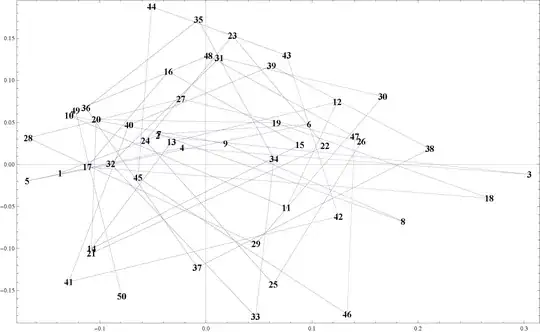
They are ordered in some sort of spiral, and I would like to join them with splines as shown below

The points are ordered clockwise (starting from 50 going backwards), and I would like the piecewise curves to be joined as smoothly as possible (doing another circuit if necessary before joining to the next point). How would I go about doing this?
Update
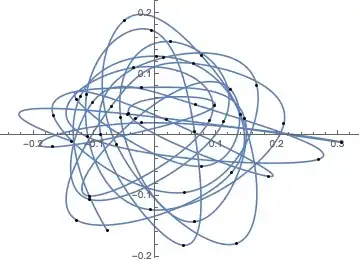
@kguler's answer is great, but doesn't join all of the points:

Is there a way to ensure the spline passes through each point?






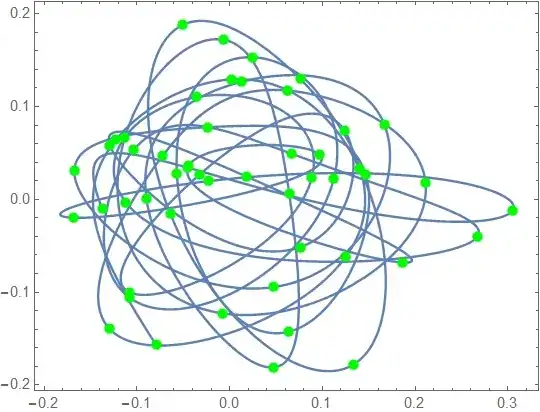

Fit[data,{1,x,x^2,x^3},x]for a cubic spline already? You could also find the convex hull for 4, 5, or 6 point sets inside your list and then model the fit to an ellipse. Then take the set of ellipses and smoothly interpolate them together. – honeste_vivere Sep 25 '14 at 13:58