Wolfgang's answer #3
It seems apropriate to create a new answer because the idea of my second answer is not taken up here.
Abstract
We present here the complete analytic solution of the problem.
First we consider the problem with the sharp step replaced by a smooth one.
Then a study of the phase space trajectories of the system will give the key insight into the solution. Here we conclude that the system stops after a finite sumber of oscillations. This also solves the tricky problem of the asymptotic behaviour of y.
Finally, the "time" dependence is calculated which completes the solution.
All this is done for the case b=0.2 but the method is general.
Smoothing out the step
Let us take instead of Sign the smooth function ArcTan so that the diffenrential equation becomes
eq = y''[x] + y[x] == -b 2/\[Pi] ArcTan[p y'[x]]
(* y[x] + (y^\[Prime]\[Prime])[x] == -((2 b ArcTan[p Derivative[1][y][x]])/\[Pi]) *)
Here the parameter p controls the steepness of the jump.
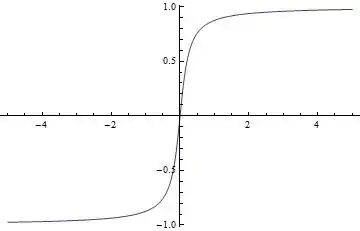
With[{p = 5}, Plot[2/\[Pi] ArcTan[p t], {t, -5, 5}]]
(* 140926_Smooth _Step.jpg *)
Solving the equation with NDSolve gives for increasing steepness
yy[x_] = With[{b = 0.2, p = 5},
y[x] /. First[
NDSolve[y''[x] + y[x] == -b 2/\[Pi] ArcTan[p y'[x]] && y[0] == 1 &&
y'[0] == -1, y[x], {x, 0, 25}]]];
Plot[yy[x], {x, 0, 25}, PlotRange -> {-1.3, 1},
PlotLabel ->
"y(x) calculated with NDSolve for smoothed-out step\nParameters: b = 0.2, p \
= 5", AxesLabel -> {"x", "y(x)"}]
(* 140926_y(x)_smooth _p _ 5.jpg *)

This lookes like a normal damped oscillation.
But now p = 50 leads to a different behaviour:
yy[x_] = With[{b = 0.2, p = 50},
y[x] /. First[
NDSolve[y''[x] + y[x] == -b 2/\[Pi] ArcTan[p y'[x]] && y[0] == 1 &&
y'[0] == -1, y[x], {x, 0, 25}]]];
Plot[yy[x], {x, 0, 25}, PlotRange -> {-1.3, 1},
PlotLabel ->
"y(x) calculated with NDSolve for smoothed-out step\nParameters: b = 0.2, p \
= 50", AxesLabel -> {"x", "y(x)"}]
(* 140926_y(x)_smooth _p _ 50.jpg *)

Now there are only three passes through zero. Afterwards y stays negative and is slowly approaching y = 0.
Letting now p=5*10^3
yy[x_] = With[{b = 0.2, p = 5*10^3},
y[x] /. First[
NDSolve[y''[x] + y[x] == -b 2/\[Pi] ArcTan[p y'[x]] && y[0] == 1 &&
y'[0] == -1, y[x], {x, 0, 25}]]];
Plot[yy[x], {x, 0, 25}, PlotRange -> {-1.3, 1},
PlotLabel ->
"y(x) calculated with NDSolve for smoothed-out step\nParameters: b = 0.2, p \
= 5,000", AxesLabel -> {"x", "y(x)"}]
(* 140926_y(x)_smooth _p _ 5k.jpg *)

Leads to a constant asymptotic values <0 for y.
yy[20]
(* -0.115909 *)
Comparing this with the sharp step
yy[x_] = With[{b = 0.2},
y[x] /. First[
NDSolve[y''[x] + y[x] == -b Sign[y'[x]] && y[0] == 1 && y'[0] == -1,
y[x], {x, 0, 25}]]];
Plot[yy[x], {x, 0, 25}, PlotRange -> {-1.3, 1},
PlotLabel ->
"y(x) calculated with NDSolve for sharp step\nParameter: b = 0.2",
AxesLabel -> {"x", "y(x)"}]
(* 140926_y(x)_sharp.jpg *)
During evaluation of In[438]:= NDSolve::mxst: Maximum number of 10000 steps reached at the point x == 11.670368725029757`. >>

shows a breakdown of NDSolve as mentioned by Michael E2 but this happens at the same constant value of y which in the smoothed-out case is extended by NDSolve to large values of x.
Now this numeric result for the asymptotic behaviour needs to be verified independently because I have shown analytically earlier for the original Sign-function that
1/2 d/dx( y'^2 + y^2 ) = - b | y' |
Which means that the quantity y'^2 + y^2 cannot grow with increasing x. At first I thought it should go to zero together with |y'|, but this is not conclusive.
Can the equation of motion have a constant solution ya?
The answer is yes: we have then y'' -> 0. This would ya -> - b Sign[y']. Now assume that for some x > x0, y' has a small positive value, i.e. Sign[y'] = +1 this leads to ya-> -b even if now y'->+0.
Now there is no contradiction: the left hand side 1/2 d/dx( y'^2 + y^2 ) -> 1/2 d/dx( 0 + y^2 ) = 1/2 d/dx( y1^2 ) = 0 and the right hand side -b |y'| -> 0 as well.
We shall make this more exact in the next section.
Phase space and asymptotics
Instead of pursuing my proposal with the piecewise trig functions (as in my soluton #2) let us look at the phase space (y, y'=v) of the problem.
The equation of motion is replaced by the system
dy/dx = v
dv/dx = - y - b Sign(v)
The trajectories in phase space are given by dividing these two equations which leads to
dv/dy = - (y + b Sign(v))/v
For v<0 we have
dv/dy = - (y - b)/v
this can be integrated to give
v^2 + (y-b)^2 = const
This means the trajectories in the lower v-plane are circles centered at (y,v) = (b,0).
The radius r1 is determined by the initial condition at x = 0: v(0) = -1, y(0) = 1, i.e.
r1 = Sqrt(1 + (1-b)^2)
Similarly, in the upper v-plane the trajectories are circles centered at (y,v) = (-b,0).
Let's draw a picture and look at the development of our example in phase space.
With[{b = .2},
r1 = Sqrt[1 + (1 - b)^2]; w = ArcCos[(1 - b)/r1];
pE = {r1 - 7 b, 0};
pD = {-r1 + 5 b, 0};
pC = {r1 - 3 b, 0};
pB = {-r1 + b, 0};
pA = {1, -1};
Show[Graphics[{Line[{{-1.2, 0}, {1.2, 0}}],
Line[{{0, -1.5}, {0, 1}}],
Point[{0, 0}], {PointSize[Medium], Point[{b, 0}],
Point[{-b, 0}]}, {PointSize[Medium], RGBColor[1, 0, 0],
Point[pA], Point[pB], Point[pC], Point[pD], Point[pE]},
Circle[{b, 0}, r1, {\[Pi], 2 \[Pi] - w}],
Flatten[Table[
Circle[{-b, 0}, Abs[r1 - (4 k - 2) b], {0, \[Pi]}], {k, 1, 2}],
1], Flatten[
Table[Circle[{b, 0}, Abs[r1 - 4 k b], {\[Pi], 2 \[Pi]}], {k, 1,
1}], 1], {Dashed,
Circle[{b, 0}, Abs[r1 - 8 b], {\[Pi], 2 \[Pi]}]},
Text["A = {1,-1}", {1, -0.9}], Text["B", {-r1 + b - 0.1, 0.1}],
Text["C", {r1 - 3 b + 0.1, 0.1}],
Text["D", {-r1 + 5 b - 0.05, 0.1}],
Text["E", {r1 - 7 b + 0.05, 0.1}], Text["-b", {-b, 0.2}],
Text["b", {b, 0.2}], Text["v", {0, 1.1}], Text["y", {1.4, 0}]}]]]
(* 140926_Graph _phase-space.jpg *)

The system point P = (y,v) moves along successive circles of given center and radius as shown in the following table
$\left(
\begin{array}{cccc}
\text{segment} & \text{center} & \text{radius} & \text{y of end point} \\
A\to B & \{b,0\} & \text{r1=Sqrt[1+(1-b)${}^{\wedge}$2]} & \text{-r1+b} \\
B\to C & \{-b,0\} & \text{r2=r1-2b} & \text{r1-3b} \\
C\to D & \{b,0\} & \text{r3=r1-4b} & \text{-r1+5b} \\
D\to E & \{-b,0\} & \text{r4=r1-6b} & \text{r1-7b} \\
\end{array}
\right)$
The journey stops at E = {r1-7b,0}. Why?
Well, as we have shown, the distance of our system point P from the origin must never increase for increasing x. This condition is indeed met along the whole path from A to E, but would be violated if P would enter the dashed circle.
Hence the asymptotic value ya of y is reached after a finite time and is given by ya = r1 - 7b = Sqrt[1+(1-b)^2] - 7b /.b->0.2 = -0.119375.
This value is now very close to the one observed with NDSolve.
I think this detailed study of the example showed all the ingredients necessary to find the asymptotic value of the solution.
It would require just more labour to explore the behaviour for other values of b, especially the number of transits and hence the sign of the asymptotic value.
Also the "time" dependence of y, i.e. y(x), can be obtained easily from the phase space trajectory integrating the equation dy/dx = v giving x(y) = Integrate[1/v[y],y].
But this integral with an integrand of the type 1/Sqrt[ r^2 - (y \[PlusMinus] b)^2] is elementary and gives an ArcSin which leads to the time dependent solution which consists of segments:
y[k](x) = \[PlusMinus] b + r[k] Sin[x + c[k]]
v[k](x) = r[k] Cos[x + c[k]]
for
x[k-1] <= x < x[k]
k = 1, 2, ..., kmax
Here r[k] are given in the table,
x[0] = 0, x[k] = Pi(k-1/2)+ArcSin[(1-b)/r[1]],
c[k] are constants determined by yk = y-value of the end point in the table.
kmax = 4 in our case.
I leave it for the interested reader to write down the explicit expressions and compare them with the previous results.
PS: I should remark that the procedure presented here improves and even replaces my solution attempt #2.
A surprisingly fascinating problem !
Regards,
Wolfgang











NDSolvefor{x, 0, 20}? – Michael E2 Sep 25 '14 at 18:52DSolvewith the numericalNDSolvewill work better.DSolveis symbolic, and thus it may take a long time (or forever) to find a symbolic solution, whereasNDSolveis numerical, and thus is not (usually) subject to such complications. – DumpsterDoofus Sep 25 '14 at 19:13