Fitting ellipse to 5 given points on the plane

Question

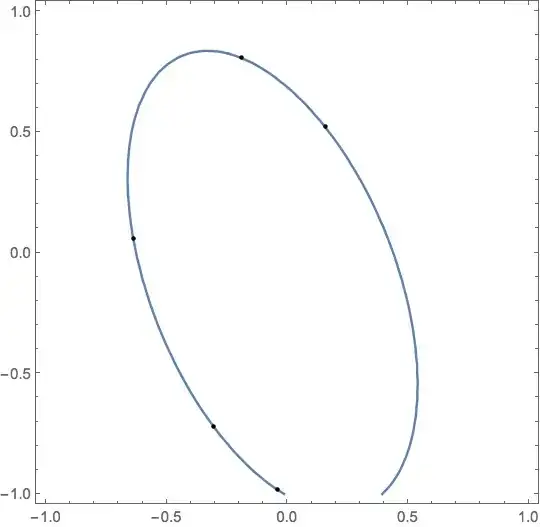
Five points are required to define a unique ellipse. An ellipse has five degrees of freedom: the $x$ and $y$ coordinates of each focus, and the sum of the distance from each focus to a point on the ellipse, or alternatively, the $x$ and $y$ coordinates of the center, the length of each radius, and the rotation of the axes about the center.

I need a function, that fits an ellipse, for given five $(x,y)$ pairs. Is there a function in Mathematica to do that? If it's possible I need a plot with the ellipse and the given points, and also the equation of the fitted ellipse.

I need an other function, that could check that if a point is on an ellipse. For example on an ellipse, that we just fitted with the previous function.

Related: http://math.stackexchange.com/questions/163920/how-to-find-an-ellipse-given-five-points — Michael E2, Sep 27 '14 at 14:20
This could be considered to be a special case of Fitting points to tilted, off-center ellipse. But it's different in that this question admits a solution that goes through all points. — Jens, Sep 27 '14 at 19:02
There is code here that will best-fit an ellipse. This is useful in cases where you want an ellipse but the given points actually determine a hyperbola. — Daniel Lichtblau, Oct 03 '14 at 21:33
See also the demonstration Five Points Determine a Conic Section. An interesting related problem is that of Small Lattice Ellipses. — TheDoctor, Oct 06 '14 at 10:37

score 30 · Accepted Answer · answered Sep 27 '14 at 13:41

30

The following is based on the fact that the determinant of a matrix is equal to zero when two rows are the same. Thus, if you plug any of the points in, you get a true statement.

SeedRandom[3];
pts = RandomReal[{-1, 1}, {5, 2}];
row[{x_, y_}] := {1, x, y, x*y, x^2, y^2};
eq = Det[Prepend[row /@ pts, row[{x, y}]]] == 0

(* Out: 
   0.0426805-0.0293168x-0.155097x^2-0.019868y-0.087933x*y-0.061593y^2 == 0
*)

ContourPlot[Evaluate[eq], {x, -1, 1}, {y, -1, 1},
  Epilog -> Point[pts]]

enter image description here

answered Sep 27 '14 at 13:41

Mark McClure

32,469
3
103
161

Thank you @Mark McClure! Can you tell me something more? Beside the Evaluate[eq] how can I plot an extra {x_6,y_6} point in the same ContourPlot? Or some extra points? – user153012 Sep 27 '14 at 17:24
@user153012 If you'd like to plot more points in a list, say morePoints, simply add another Point primitive containing your list to the Epilog. – Mark McClure Sep 27 '14 at 18:53
@user153012 For more than five points, see my comment to the original question: it becomes a fitting problem that has been asked about before. – Jens Sep 27 '14 at 19:05
@Jens Thank you. The referred question is interesting. I know for $5$ points it is a special case of that. But this last question is a little bit different, because I wanted to plot extra points, after we determined the ellipse. – user153012 Sep 27 '14 at 19:07
@Jens My assumption is that the OP simply wants to add more points that are know to be on the same ellipse, rather than find a best fit. – Mark McClure Sep 27 '14 at 19:08
@MarkMcClure Looks like your assumption is correct (of course I already upvoted your answer). – Jens Sep 27 '14 at 19:09

score 11 · Answer 2 · edited Oct 31 '20 at 20:49

11

The general equation of an ellipse (here) is given by:

ellipse[x_, y_] = a x^2 + b x y + c y^2 + d x + e y + f == 0;

solving using 5 points results in:

SeedRandom[3];
pts = RandomReal[{-1, 1}, {5, 2}];
sol = Solve[ellipse @@@ pts];
ellipse[x, y] /. sol[[1]] // Simplify
(a (-0.275185 + 1. x^2 + x (0.189022 + 0.566953 y) + 0.1281 y + 
    0.397124 y^2) == 0)

all $a$ values result in the same equation except when $a=0$.

edited Oct 31 '20 at 20:49

brainjam

259
1
9

answered Sep 28 '14 at 00:06

Basheer Algohi

19,917
1
31
78

With MMA V9 I do not get the right answer, for example f (-0.275185 + 1. x^2 + x (0.189022 + 0.566953 y) + 0.1281 y + 0.397124 y^2) == 0 is the equation of the ellipse which is returned. The parameter f is not resolved. – Sigis K Oct 01 '14 at 12:02
it is the same except a is replaced by f. – Basheer Algohi Oct 01 '14 at 13:47
1

Your ellipse definition is in fact the general equation of a conics - it is only an ellipse if the discriminant is negative. How does your answer take this restriction into account? Thanks – Sigis K Oct 01 '14 at 22:08

Narasimham · Answer 3 · 2014-10-03T20:42:12.217

2

Through 5 points we can pass a conic, an ellipse, hyperbola etc. After Algohi's solution coefficients are obtained we can determine choice of conic by sign of the second evaluated invariant $ (b^2 - 4 a c) $ along with standard calculated expression for values of rotation/translation of central conic.A sign change test for a test point chosen inside or outside can be done,it should vanish on the arc.

edited Oct 03 '14 at 20:42

answered Oct 03 '14 at 20:27

Narasimham

3,160
13
26

Fitting ellipse to 5 given points on the plane

3 Answers3

Linked