I am trying to do a first order interpolation on a multidimensional data set containing duplicate abscissa values (which Mathematica does not like), like this one:
{{{1, 2, 3}, 10}, {{1, 2, 3}, 20}, {{1, 2, 4}, 30}}
After playing around with DeleteDuplicates and Union I found that DeleteDuplicates does not work on multidimensional data, at least not when represented like above. I found that Union could delete the duplicates by using the SameTest-option, like this:
Union[{{{1, 2, 3}, 10}, {{1, 2, 3}, 20}, {{1, 2, 4}, 30}}, SameTest -> (#1[[1]] == #2[[1]] &)]
which returns
{{{1, 2, 3}, 10}, {{1, 2, 4}, 30}}
However, it is very slow with larger data sets, which I have, so that is not an option.
What I really would like is a function that will make an average of the duplicates, so that
{{{1, 2, 3}, 10}, {{1, 2, 3}, 20}, {{1, 2, 4}, 30}}
will turn into
{{{1, 2, 3}, 15}, {{1, 2, 4}, 30}}
I am by no means an expert in Mathematica programming, so I could really use some help.
The solution has to be reasonable fast. My data set is not sorted in any way but I guess it can be sorted quickly before the duplicates are combined if that is needed.
Thanks in advance :-)

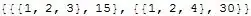

SameTesthas been addressed many times on this site; personally here at least: (17041), (21711), (28696), (30328). The second part, the actual question, I believe to be yet another duplicate of (4332) – Mr.Wizard Sep 29 '14 at 15:53