3

I use Mathematica to implement the de Casteljau algorithm

$$\vec{P}_{k,i}(u_0)=(1-u_0)\vec{P}_{k-1,i}(u_0)+u_0\vec{P}_{k-1,i+1}(u_0)$$

The graphics that de Casteljau algorithm generated as follows:

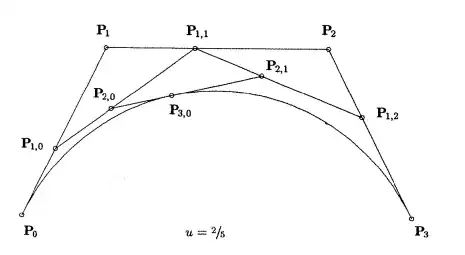
diagram

My trial

(*The recursion formula*)
P[k_, i_, u0_] :=
 (1 - u0) P[k - 1, i, u0] + u0 P[k - 1, i + 1, u0]
(*Initial values*)
P[0, 0, 2/5] = {0, 0};
P[0, 1, 2/5] = {2, 4}; 
P[0, 2, 2/5] = {4, 5};
P[0, 3, 2/5] = {6, 0};

ptsData = Table[P[k, i, 2/5], {k, 0, 3}, {i, 0, 3 - k}];
pts = {{0, 0}, {2, 4}, {4, 5}, {6, 0}};
Graphics[
  Join[Point /@ ptsData, Line /@ ptsData, {Red, BezierCurve[pts]}]]

It works well.

yes it does

So I packed these codes to a function deCasteljau[]

deCasteljau[pts_, u_] :=
 Module[{p, ptsdata, n},
  n = Length@pts - 1;
  Table[p[0, j, u], {j, 0, n}] = pts;
  p[k_, i_, u0_] :=(1 - u0) p[k - 1, i, u0] + u0 p[k - 1, i + 1, u0];
  ptsdata = Table[p[k, i, u], {k, 0, n}, {i, 0, n - k}];

Graphics[
   Join[Point /@ ptsdata, Line /@ ptsdata, {Red, BezierCurve[pts]}]]
]

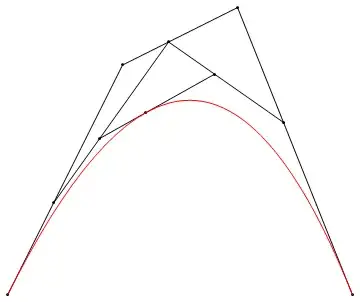
However, it failed.

deCasteljau[{{0, 0}, {2, 4}, {4, 5}, {6, 0}}, 2/5]

errors

I felt that the main question is the recursion formula p[k_, i_, u0_] :=(1 - u0) p[k - 1, i, u0] + u0 p[k - 1, i + 1, u0]; But I cannot deal with it by myself smoothly.

Question:

How to revise it?(Or how to avoid using the recursion formula. Namely, using Mathematica construction to replace it)

Edit

Thanks for kale help

When I input

 ?j

 Global`j

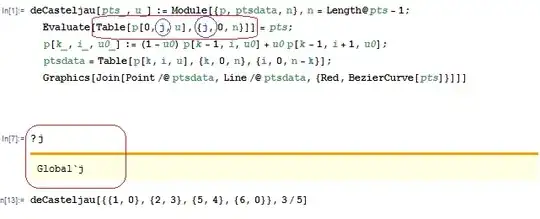
result

In general, the variable j in construction Table[p[0, j, u], {j, 0, n}] should be local.

Community
  • 1
xyz
  • 605
  • 4
  • 38
  • 117

2 Answers2

7

Set has attributes HoldFirst. So when we evaluate a=2 (aka Set[a,2]), a is held until the rhs is evaluated.

In your example, the issue is setting your initial points with Table[p[0, j, u], {j, 0, n}] = pts;. We can add Evaluate and get along with our business. This forces the Table command to evaluate first before proceeding with Set.

deCasteljau[pts_, u_] := Module[{p, ptsdata, n}, n = Length@pts - 1;
 Evaluate[Table[p[0, j, u], {j, 0, n}]] = pts;
 p[k_, i_, u0_] := (1 - u0) p[k - 1, i, u0] + u0 p[k - 1, i + 1, u0];
 ptsdata = Table[p[k, i, u], {k, 0, n}, {i, 0, n - k}];
 Graphics[
 Join[Point /@ ptsdata, Line /@ ptsdata, {Red, BezierCurve[pts]}]]
]

deCasteljau[{{0, 0}, {2, 4}, {4, 5}, {6, 0}}, 2/5]

enter image description here

kale
  • 10,922
  • 1
  • 32
  • 69
  • +1, Could you tell me why j in Evaluate[Table[p[0, j, u], {j, 0, n}]] = pts; is Global, not local – xyz Oct 01 '14 at 03:04
  • @Tangshutao It's not Global. It's localized inside of the Table function. I'm definitely not an expert in this but it appears the presence of j is made known, but no values are assigned. Table effectively uses Block so even if j had a global value assigned, the Table construct would still work as desired. – kale Oct 01 '14 at 14:17
  • The syntax colorof j is black when j has a value outsize – xyz Oct 01 '14 at 14:38
  • @Tangshutao But the Table construct still works, meaning (IMO) it's a bug with the syntax coloring engine. – kale Oct 01 '14 at 15:07
  • So @kale I use the P[0, #, u] & /@ Range[0, n] to replace it. – xyz Oct 01 '14 at 15:09
2

Although I cannot understand why j in Evaluate[Table[p[0, j, u], {j, 0, n}]] = pts is Local, I use P[0, #, u] & /@ Range[0, n] to avoid using Table[p[0, j, u], {j, 0, n}]

With the help of kale, I improve my function deCasteljauPlot[] as below:

deCasteljauPlot[pts : {{_, _} ..}, u_?NumericQ, opts : OptionsPattern[Plot]] :=
 Module[{P, ptsCoordi, n}, 
  n = Length@pts - 1;  
  (*Assign initial values *)
  Evaluate[P[0, #, u] & /@ Range[0, n]] = pts;
  (*recursion formula*)
  P[k_, i_, u0_] := (1 - u0) P[k - 1, i, u0] + u0 P[k - 1, i + 1, u0];
  (*generate the coordinates of points*)
  ptsCoords = Table[P[k, i, u], {k, 0, n}, {i, 0, n - k}];
  Graphics[
   Join[
    {PointSize[.012], Red}, Point /@ ptsCoords, {Black}, 
     Line /@ ptsCoords, {Red, BezierCurve[pts]}],
  (*generate the names of points*)
    Epilog ->
     Text @@@
      Join[
       Thread@
        {Table[Style[Subscript["P", i], 12, Blue], {i, 0, n}], 
         # + {.2, .2} & /@pts},
       Thread@
        {Flatten@
          Table[Style[Subscript["P", k, i], 12, Purple], 
                {k, 1, n}, {i,0, n - k}],             
          # + {.2, .2} & /@ Flatten[Rest@ptsCoordi, 1]}], opts]
  ]

Test

 deCasteljauPlot[{{0, 0}, {2, 4}, {4, 5}, {6, 0}}, 2/5, 
                  PlotRange -> {{-1, 9}, {-1, 6}}, ImageSize -> 500]

enter image description here

Or we can Manipulate to look the process

Manipulate[
  deCasteljauPlot[
    {{0, 0}, {2, 4}, {4, 5}, {6, 0}}, u, 
    PlotRange -> {{-1, 7}, {-1, 6}}, ImageSize -> 400], 
  {{u, .2}, 0, 1}
]

enter image description here

xyz
  • 605
  • 4
  • 38
  • 117