Given a matrix, A:
A = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
How can I do the matrix multiplication A times A step by step?
Given a matrix, A:
A = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
How can I do the matrix multiplication A times A step by step?
If you have Mathematica 10 you can use the new Inactive functionality
step1 = MatrixForm[Inner[Inactive[Times], A, A, Inactive[Plus]], TableSpacing -> {3, 3}]

step2 = Activate[step1, Times]

Activate[step2]

Inactivate on Plus and Times to get this to work with Inner, but it wasn't working because I was placing Inactive at the wrong locations of my expression. +1 for getting it to work!
– DumpsterDoofus
Oct 05 '14 at 16:19
You can use HoldForm or Defer with Composition if you are still using Pre V10 versions:
MatrixForm[Inner[Composition[Defer, Times], A, A,
Composition[Defer, Plus]], TableSpacing -> {3, 3}]
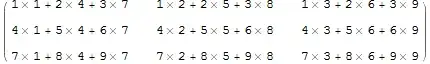
MatrixForm[Inner[Times, A, A, Composition[HoldForm, Plus]], TableSpacing -> {3, 3}]

MatrixForm[Inner[Times, A, A, Plus], TableSpacing -> {3, 3}]

Of course, there's the V10 syntax for Composition i.e. @* that can make the above code shorter:
MatrixForm[Inner[Defer@*Times, A, A, Defer@*Plus], TableSpacing -> {3, 3}]
MatrixForm[Inner[Times, A, A, Defer@*Plus], TableSpacing -> {3, 3}]
MatrixForm[Inner[Times, A, A, Plus], TableSpacing -> {3, 3}]
Clear[A, n, k, nn, aa]
A = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
Print["A"]
MatrixForm[A]
aa = Length[A];
Print["First step in matrix multiplication A times A"]
MatrixForm[
Table[Flatten[
Table[Table[
StringJoin[{"(", ToString[A[[nn, k]]], ")", "\[CenterDot]", "(",
ToString[A[[k, n]]], ")",
If[k < aa, "+", If[n == aa, "", ","]]}], {k, 1, aa}], {n, 1,
aa}]], {nn, 1, aa}]]
Print["Multiply:"]
MatrixForm[
Table[Flatten[
Table[Table[
StringJoin[{"(", ToString[A[[nn, k]]*A[[k, n]]], ")",
If[k < aa, " +", If[n == aa, "", ", "]]}], {k, 1, aa}], {n,
1, aa}]], {nn, 1, aa}]]
Print["and add:"]
MatrixForm[A.A]
Not a symbolically pure method but it does the job if one accepts that the terms are prepended with an empty space "" and wrapped with two square brackets [ ].
A = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
B = Table[Table[""[A[[n, k]]], {k, 1, Length[A]}], {n, 1, Length[A]}];
TableForm[B.B]
A = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}; B = A; TableForm[ Table[Table[Sum[A[[n, i]]*B[[i, k]], {i, 1, Length[A]}], {k, 1, Length[A]}], {n, 1, Length[A]}]]
– Mats Granvik
Feb 14 '21 at 09:13
One can get (more drawn out) steps with the WolframAlpha command:
WolframAlpha["{{1,2,3},{4,5,6},{7,8,9}}.{{1,2,3},{4,5,6},{7,8,9}}",
{{"Result", 2}, "Content"}, PodStates -> {"Result__Step-by-step solution"}]