Bad performance from SubsetQ?

Question

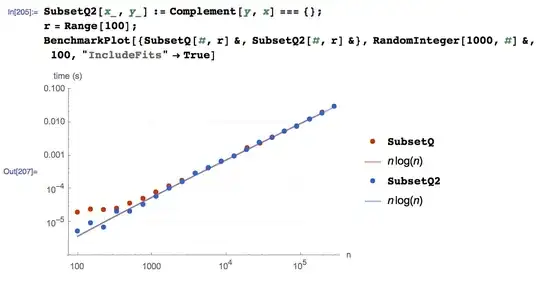
Can I say this is a bad performance from the new V10 function SubsetQ?

Here are some tests comparing it to Complement[l2, l1] === {}

count1[data_,list_]:=Module[{r},
   r=SubsetQ[#,list]&/@data;
   Counts[r]
]

count2[data_,list_]:=Module[{r},
    r=Complement[list,#]==={}&/@data;
    Counts[r]
]

Small columns test:

$HistoryLength = 0;
data = RandomInteger[100, {100000, 10}];
list = {4, 3, 2, 1};

count1[data, list] // AbsoluteTiming
count2[data, list] // AbsoluteTiming

{2.760775, <|False -> 99995, True -> 5|>} {0.450933, <|False -> 99995,True -> 5|>}

Large columns test:

$HistoryLength=0;
data=RandomInteger[100,{100000,100}];
list={4, 3, 2, 1};

count1[data,list]//AbsoluteTiming
count2[data,list]//AbsoluteTiming

{3.345720, <|False -> 97745, True -> 2255|>} {0.910420, <|False -> 97745, True -> 2255|>}

Update:

Still slow in V10.1

Answer 1

SubsetQ is implemented in top-level using Complement[a, b] === {}. It has some overhead because it has to treat associations specially, plus it has to go through the requisite error-handling rigmarole. But has the same time complexity in the length of the first argument:

But this is on the shortlist of functions to reimplement in C when we have time. There are other patients that are more worthy of the "Vitamin C" treatment, however :).

Answer 2

EDIT

After comments from RunnyKine...

Just another approach and timing:

subs[u_, v_] := Length@Intersection[u, v] == Length@v

Performance:

 BenchmarkPlot[{count1[#, list] &, count2[#, list] &, 
 Tally@Map[Function[x, subs[x, list]], #] &}, 
 RandomInteger[100, {100000, #}] &, PowerRange[1, 1000], 
 "IncludeFits" -> True, Frame -> True]