Calculate inertia tensors

Question

Moments of inertia and inertia tensors are well-known characteristics of rigid bodies in physics and applied mathematics. How to calculate them in Mathematica? Is possible to use regions which was introduced recently in version 10?

Maybe of interest: I used the inertia tensor to identify symmetries of an object in an image in this answer. — Jens, Oct 12 '14 at 00:54
I was going to say that I was almost positive that the Wolfram Mathematica 10 product page had a splash-screen where they showed a rendering of a human tooth and overlayed it with the principle axes and labeled it with the eigenvalues of the inertia tensor, and then I saw you answered your question, hehe. +1 — DumpsterDoofus, Oct 12 '14 at 14:10
There is also SolidData["Steinmetz2Solid", "InertiaTensor"] and friends, although I think it only works for named solids, and not arbitrary regions. — DumpsterDoofus, Oct 12 '14 at 14:13

score 19 · Answer 1 · answered Oct 11 '14 at 23:24

The inertia tensor is defined as an integral of the following tensor over the body region

vars = {x, y, z};
r2 = IdentityMatrix[3] Tr[#] - # &@Outer[Times, vars, vars];
r2 // MatrixForm

enter image description here

It is very simple to do with integration over a region

Integrate[r2, vars ∈ region]

It can be wrapped in the following function

inertiaTensor[reg_, assum_: {}] := 
  Module[{x, y, z, d = RegionEmbeddingDimension[reg], r2, vars},
   vars = {x, y, z};
   r2 = IdentityMatrix[3] Tr[#] - # &@Outer[Times, vars, vars];
   If[d == 2, r2 = r2 /. z -> 0; vars = {x, y}];
   If[d == 1, r2 = r2 /. {x -> 0, y -> 0}; vars = {z}];
   Integrate[r2, vars ∈ reg, Assumptions -> assum]/
     Integrate[1, vars ∈ reg, Assumptions -> assum] // 
    Simplify];

I assume that the body have a unit mass. I also assume that 2D bodies lie in xy plane and 1D bodies lie on the axes z.

Now we can prepare the following demonstration which corresponds to known list of moments of inertia

gr3d = Graphics3D[{PointSize[0.03], Thickness[0.03], 
     FaceForm[Opacity[0.5]], Blue, #, Gray, Thickness[0.01], 
     Line[{-#, #} & /@ IdentityMatrix[3]], Black, 
     Text @@@ {{x, {1.1, 0, 0}}, {y, {0, 1.1, 0}}, {z, {0, 0, 1.1}}}},
     ImageSize -> 150, PlotRange -> 1, Boxed -> False, 
    SphericalRegion -> False, ViewAngle -> Pi/10] &;
gr2d = gr3d@{FaceForm[Opacity[1]], Texture[#], EdgeForm[None], 
         Polygon[{{-1, -1, 0}, {1, -1, 0}, {1, 1, 0}, {-1, 1, 0}}, 
          VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 
             1}}]} &@Rasterize[#, Background -> None] &@
    Graphics[{EdgeForm[Blue], FaceForm[{Opacity[0.5], Blue}], 
      Blue, #}, PlotRange -> 1.01, ImageSize -> 150, 
     Background -> Transparent] &;

Manipulate[
   Row@{type[[1]], 
     MatrixForm[m inertiaTensor @@ type[[2 ;;]]]}, {type, 
    Thread[#[[All, 2 ;;]] -> #[[All, 1]]]}, 
   Initialization :> {type = #[[1, 2 ;;]]}] &@{{"Point", 
   gr3d@Point[{0, 0, 1}], Point[{0, 0, r}], r > 0},
  {"Rod", gr3d@Line[{{0, 0, -1/2}, {0, 0, 1/2}}], 
   Interval[{-a/2, a/2}], a > 0},
  {"Circle", gr2d@Circle[], Circle[{0, 0}, r], r > 0},
  {"Disk", gr2d@Disk[], Disk[{0, 0}, r], r > 0},
  {"Cylinder", gr3d@Cylinder[{{0, 0, -1/2}, {0, 0, 1/2}}, 1/2], 
   Cylinder[{{0, 0, -h/2}, {0, 0, h/2}}, r], {r > 0, h > 0}},
  {"Tetrahedron", gr3d@Tetrahedron[#], Tetrahedron[s #], s > 0} &@
   PolyhedronData["Tetrahedron", "VertexCoordinates"],
  {"Sphere", gr3d@Sphere[], Sphere[{0, 0, 0}, r], r > 0},
  {"Ball", gr3d@Ball[], Ball[{0, 0, 0}, r], r > 0},
  {"Cone", gr3d@Cone[{{0, 0, 2/3}, {0, 0, 0}}, 1/2], 
   Cone[{{0, 0, h}, {0, 0, 0}}, r], {r > 0, h > 0}},
  {"Ellipsoid", gr3d@Ellipsoid[{0, 0, 0}, {0.7, 0.5, 0.3}], 
   Ellipsoid[{0, 0, 0}, {a, b, c}], {a > 0, b > 0, c > 0}},
  {"Rectangle", gr2d@Rectangle[-{1, 1}/2, {1, 1}/2], 
   Rectangle[-{a, a}/2, {a, a}/2], a > 0},
  {"Cuboid", gr3d@Cuboid[-{0.4, 0.3, 0.2}, {0.4, 0.3, 0.2}], 
   Cuboid[-{a, b, c}/2, {a, b, c}/2], {a > 0, b > 0, c > 0}}}

enter image description here

Good afternoon! I invite you to think about the problem. I'm in love with her now, but I haven't received a decision yet https://mathematica.stackexchange.com/questions/277997/inertia-tensors-for-non-typical-rigid-bodies — dtn, Dec 31 '22 at 07:42

score 7 · Accepted Answer · answered Mar 23 '16 at 05:39

In Mathematica 10.4, MomentOfInertia is now built-in. So we can compute inertia tensor for named, arbitrary and formula regions. Some examples:

MomentOfInertia[Ball[]]

(* {{(8 Pi)/15, 0, 0}, {0, (8 Pi)/15, 0}, {0, 0, (8 Pi)/15}} *)

reg = DelaunayMesh[RandomReal[1, {20, 3}]]

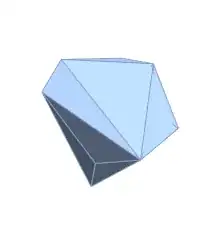
Mathematica graphics

MomentOfInertia[reg]
(* {{0.0227787, 0.085264, 0.0937136}, {0.085264, 0.0226137, 
  0.0801547}, {0.0937136, 0.0801547, 0.0183785}} *)

score 2 · Answer 3 · edited Mar 23 '16 at 05:50

2

For the Cuboid is wrong the right answer is

{"Cuboid", gr3d@Cuboid[-{0.4, 0.3, 0.2}, {0.4, 0.3, 0.2}], 
 Cuboid[-{b, b, b}, {b, b, b}], {b > 0, b > 0, b > 0}}}

because the sides are equal

edited Mar 23 '16 at 05:50

bbgodfrey

61,439
17
89
156

answered Mar 23 '16 at 05:12

Pichuz Üribe

21
1

5

Please provide more detail. – bbgodfrey Mar 23 '16 at 05:51

Calculate inertia tensors

3 Answers3

Linked